DOPPLERŮV JEV

Fyzika Dopplerova jevu

Dopplerův jev lze popsat jako změnu frekvence vlny v závislosti na pohybu jejího vysílače a/nebo příjemce. Klasickým příkladem užívaným k vysvětlení Dopplerova jevu je sanitka projíždějící kolem pozorovatele. Rychlostí vozu se kmitočet zvukové vlny před autem zvyšuje a za autem snižuje. Pozorovatel vnímá pak tento jev jako rozdílně vysoký tón houkačky: Než k němu sanitka přijede, je tón vyšší, jakmile se od něj sanita vzdaluje, je tón nižší.

Kmitočet se mění v závislosti na prostředí, ve kterém se vysílač a/nebo příjemce pohybuje (např. ve vzduchu). Ve svém standardním díle „Ueber das farbige Licht der Dopplersterne und einiger anderer Gestirne des Himmels“ [„O barevném světle dvojhvězd a některých jiných hvězd na nebi“] vydaném v roce 1842 uvedl Doppler následující rovnici k výpočtu kmitočtu vnímaného přijímačem.

V této rovnici platí:
   frekvence vnímaná příjmačem
   frekvence vysílaná zdrojem
  rychlost přijímače v relativním poměru k prostředí
   rychlost zdroje v relativním poměru k prostředí a
   rychlost šíření vlny v prostředí (rychlost zvuku)

Případ 1: stacionární přijímač, pohyblivý vysílač: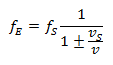

Případ 2: stacionární vysílač, pohyblivý příjemce: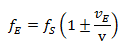

Obě tyto rovnice popisují klasický Dopplerův jev. Podle nich je působení změny kmitočtu závislé na rychlosti, kterou se v relativním poměru pohybuje vysílač a přijímač v prostředí šíření vlny. V Dopplerově době to představovalo revoluční poznatek. Ve své původní publikaci Doppler píše: „Od těchto čistě subjektivních ustanovování, nikoliv od objektivních skutkových stavů, je odvislá barva a intenzita vnímání světla nebo výška a síla zvuku.“

 

Dopplerův jev a světlo

Christian Doppler vycházel z toho, že tento jev platí pro všechny druhy vlnění. Tehdejší vědecký názor předpokládal, že také světlo potřebuje pro své šíření určité prostředí (médium), jehož vlastnosti ovšem nebyly známé a které bylo označováno jako „éter“. Až v roce 1881, resp. 1887 fyzikové Albert A. Michelson a Edward W. Morley experimentálně prokázali, že žádný takový éter plnící funkci prostředí pro šíření světla neexistuje (Michelsonův-Morleyův experiment). Dnes víme, že klasický Dopplerův jev platí jen pro vlnění, které se šíří v určitém prostředí.

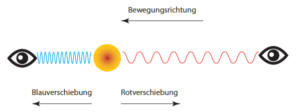
Dopplerův jev se ale přesto týká též elektromagnetických vln, jakými je i světlo a jež pro své šíření nepotřebují žádné médium. Dochází ke změně barvy – směrem k modrému spektru, jestliže se vysílač blíží k přijímači a vlny jsou „zhušťovány“, a v opačném případě dochází k výslednému rudému posuvu, jelikož se vlny „roztahují“ (viz obrázek).

U elektromagnetických vln tento jev ovšem nezávisí na relativním pohybu mezi prostředím umožňujícím šíření a přijímačem, resp. vysílačem, nýbrž pouze na relativním pohybu mezi přijímačem a vysílačem. Dopplerův jev popisující změnu vlnové délky světla se z toho důvodu označuje jako relativistický Dopplerův jev. Pro elektromagnetické vlny platí, že přijímaná frekvence stojí k vysílané frekvenci v následujícím poměru:

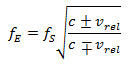
V této rovnici pro relativistický Dopplerův jev značí c rychlost světla 299 792 km/s a relativní rychlost mezi vysílačem a přijímačem.

Praktická aplikace Dopplerovy rovnice

V následujících příkladech si ukážeme dva specifické případy šíření zvukových vln ve vzduchu, přičemž v předešlé části vysvětlené proměnné dosadíme do Dopplerovy rovnice jako odpovídající frekvenci a rychlost.

Případ 1: Přijímač je v klidu relativně ke vzduchu, vysílač (zdroj zvuku) se pohybuje rychlostí směrem k přijímači (-) nebo od přijímače (+).

Pro tento případ platí tato Dopplerova rovnice:

Příklad: Řidič auta (vysílač zvukových vln) projíždí rychlostí 130 km/h (~36 m/s) kolem chodce stojícího na kraji vozovky (přijímač zvukových vln). Protože se řidič auta a chodec dobře znají, zdraví řidič auta chodce dlouhým zatroubením. Výška tónu zatroubení vykazuje kmitočet 1 000 Hz. Jakou výšku zvuku chodec uslyší?

Chodec slyší během přibližování auta výšku tónu o frekvenci:

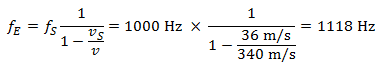
Jestliže se auto od přijímače vzdaluje, výška tónu klesá:

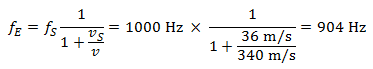
Znamená to, že se výška tónu během přibližování auta zvyšuje o 118 Hz a naopak se při jeho vzdalování snižuje o 96 Hz. Hodnota 1 000 Hz odpovídá jako tón přibližně vysokému c’’’, které se do notového systému zapisuje na druhou linku nad notovou osnovou. Změny výšky tónu během přibližování a vzdalování auta jsou v tomto případě jen nepatrně rozdílné, poněvadž rozdíl výšky tónu činí přibližně jen jeden půltón.

Případ 2: Vysílač (zdroj zvuku) je v klidu relativně ke vzduchu, přijímač se pohybuje rychlostí směrem k vysílači či směrem (+) od vysílače (-).

Dopplerovu rovnici zapíšeme v tomto případě takto:

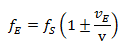
Příklad: Řidič auta je příjemcem a projíždí kolem známého stojícího na kraji vozovky (vysílač) rychlostí 130 km/h (~36 m/s). Známý má s sebou náhodou houkačku a pozdraví projíždějícího dlouhým tónem o frekvenci 1 000 Hz.

Řidič auta slyší při přibližování tón o frekvenci:

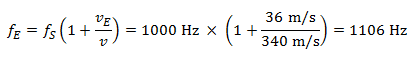
Při vzdalování se od chodce slyší řidič tón o frekvenci:

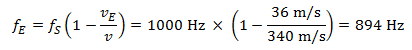
V tomto případě je přijímačem (resp. příjemcem – řidičem auta) zaznamenaná změna výšky tónu během přibližování i vzdalování auta od houkajícího známého stejná, totiž vždy 106 Hz.

Důvodem pro rozdíl při změnách frekvencí v těchto obou případech je, že zvuk potřebuje pro své šíření médium. Tím je v těchto příkladech vzduch v okolí. V případě 1 se vysílač (zdroj zvuku) pohybuje relativně ke vzduchu, v případě 2 je to přijímač.  

Použitý materiál čerpá z knihy:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger (Christian Doppler – Pro lidstvo nejdůležitější Salcburčan) Clemens M. Hutter, Verlag Anton Pustet 2017

 

Jiný pohled na Dopplerův jev

Všichni znají Dopplerův jev! Opravdu?

Více než 150 let předtím, než Christian Doppler popsal jev, který po něm byl pojmenován, a formuloval ho ve vzorcích, použil ho O. Rømer a jeho kolegové k určení rychlosti světla.

Jedná se o obecné znalosti fyziky, že Dopplerův jev spočívá v posunu frekvencí, když se vysílač a přijímač vln vůči sobě pohybují. Tento fenomén nese informaci o jejich vzájemném pohybu.

Ale potřebujeme opravdu vlny ke komunikaci mezi zdrojem a pozorovatelem? Ne. Představte si maják otáčející se pevně danou frekvencí a vyzařující silný rovnoběžný paprsek světla. Nehybný pozorovatel v nějaké vzdálenosti od majáku uvidí pulzy s rovnoměrnými intervaly. Uvážíme-li však jiného pozorovatele, který se přibližuje či vzdaluje, bude se mu frekvence pulzů jevit vyšší či nižší – stejně jako frekvence světelné vlny popsané „klasickým“ Dopplerovým jevem. V praxi je tento jev sotva patrný, protože pozorovatelé (např. lodě) se pohybují jen pomalu. V astronomii byl však užitečný po staletí…

Koncem 17. století byly oběžné rychlosti a dráhy planet kolem Slunce (a tedy i relativní rychlosti jednotlivých planet) dobře známy díky Keplerovým zákonům.

Galileo objevil čtyři největší měsíce Jupiteru. Čas, který je zapotřebí k dokončení celého oběhu nejvnitřnějšího z těchto měsíců Io, se dá měřit pomocí jeho zmizení a zjevení zpoza Jupiteru. Po několika letech pečlivého měření se naskytla variace oběžné rychlosti, která se měnila v průběhu roku! Protože však nebylo pochybnosti o správnosti Newtonových zákonů, bylo potřeba jiné vysvětlení.

Ole Rømerovým skvělým nápadem bylo, že světlo přicházející z Io se pohybuje pevnou rychlostí: variace v pozorované oběžné rychlosti by tedy byly způsobeny relativní rychlostí Země vůči Jupiteru, která se v průběhu roku měnila.

Země je ke Slunci blíže než Jupiter, obíhá kolem Slunce tedy rychleji. V jeden moment se může k Jupiteru přibližovat, jindy zase oddalovat. Dříve zmíněný majákový jev tedy hraje roli i v případě Galileova pozorování měsíce Io. Ole Rømer tohoto poznatku využil pro určení rychlosti světla. První určení rychlosti světla nebylo příliš přesné, ale řádově správné, což některé fyziky v té době šokovalo.

Jeden z novějších příkladů můžeme nalézt v současné astronomii. Pulsar PSR1913+16 je neutronová hvězda otáčející se sedmnáctkrát za sekundu kolem své osy a kvůli tomu vysílá rádiové impulsy v dobře definovaném kuželu. Když tento kužel protne Zemi, naše radioteleskopy zachytí rádiový impuls trvající několik milisekund. Pokud by tento pulsar (ve vzdálenosti 22000 světelných let od Slunce) byl stacionární, měnila by se frekvence pulzů pouze kvůli oběhu Země kolem Slunce. Nicméně, tyto variace jsou mnohem častější a mohutnější, než bychom čekali.

To, čeho astronomové na konci 17. století dosáhli, opakovali v druhé polovině 20. století Russel Hulse a Joseph Taylor. Variace v časech dopadu radiových pulzů z PSR1913+16 vysvětlili hypotézou, že tento pulsar tvoří binární systém s další neutronovou hvězdou. Obě hvězdy se otáčí kolem společného gravitačního středu na eliptických oběžných drahách s periodou 7.75 hodiny. V bodě, kdy jsou si nejblíže, je jejich vzájemná rychlost čtyřikrát větší než v bodě, kdy jsou si nejvzdálenější – to je ideální pro sledování variací časů dopadu jednotlivých rádiových pulzů, které reprezentují „majákové signály“ pro tento Dopplerův jev.

Tento binární systém je pozorován již přes 50 let a měření jsou natolik přesná, že představují „modelový systém“ pro efekty popsané obecnou teorií relativity, např. relativně rychlou precesi orientace eliptických drah a jejich „smršťování“, tj. ztrátu energie vyzařováním gravitačních vln. Za jejich měření a interpretaci byli Hulse a Taylor odměněni Nobelovou cenou za fyziku v roce 1993. Radiové pulzy tvořené PSR1913+16 reprezentují jedny z nejpřesnějších hodin dnešní doby a pomáhají nám přesněji měřit rychlost Slunce kolem středu naší galaxie.

Na první pohled nemusí být rozdíl mezi „klasickým“ a „majákovým“ Dopplerovým jevem zřejmý. Skutečnost, že při majákovém jevu je nosičem signálu elektromagnetická vlna (viditelné světlo u Io nebo širokopásmové radiové signály z PSR1913+16), může přispívat ke zmatkům. Nicméně co majákový jev měří, nejsou (téměř neměřitelné) variace ve frekvencích záření, nýbrž přesné doby dopadu těchto signálů. Aby toto měření bylo smysluplné, musí být délka signálu mnohokrát kratší než intervaly mezi pulzy. (Tak je tomu ve dvou výše uvedených příkladech). Pokud se pozorovatel blíží k majáku pevnou rychlostí, budou intervaly mezi dvěma po sobě jdoucími impulsy kratší než ve stacionárním případě, protože světlo musí urazit stále kratší vzdálenost mezi dvěma po sobě jdoucími pozorováními.

Astronomové volně používají termín „Dopplerův jev“, když mluví o časových změnách signálů v závislosti na relativním pohybu vysílače a přijímače.  Někteří fyzici se proti tomuto použití ohrazují, protože se domnívají, že tento efekt je omezen pouze na změny frekvence vlnění. Účelem měření je vždy určení relativní rychlosti vysílače vůči přijímači, nezáleží tedy, zda se použije vlnový nebo majákový signál. Obě techniky si zaslouží označení „Dopplerův jev“, i když sám Doppler si toto použití v širším kontextu možná nepředstavoval. Doppler ve svém původním článku prezentovaném v roce 1842 hovořil o „vlnových nárazech“ a vzorce odvodil z rozdílu počtu kmitů za jednotku času pro vysílač a přijímač Vzorce tedy platí pro jakékoliv zdroje „vlnových nárazů“ tedy i pro „majákový“ Dopplerův jev.

Further information on the Doppler effect | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
² https://de.wikipedia.org/wiki/PSR_J1915%2B1606

Překlad: Sedláček Ondřej