Doppler-Effekt

Die Physik des Doppler-Effekts

Der Doppler-Effekt beschreibt die Änderung der Frequenz einer Welle und zwar abhängig vom Bewegungszustand ihres Senders und/oder Empfängers. Das klassische Beispiel, um den Doppler-Effekt zu erklären, ist ein Krankenwagen, der an einem Beobachter vorbeifährt. Durch die Bewegung des Wagens werden die Schallwellen vor dem Auto gestaucht und hinter dem Auto gedehnt. Der Beobachter nimmt diesen Effekt dann durch die unterschiedliche Tonhöhe des Martinshorns wahr: Bevor der Krankenwagen ihn erreicht hat, ist der Ton höher, sobald der Wagen sich von ihm entfernt, ist der Ton tiefer.

Je nachdem, ob sich Sender und/oder Empfänger in einem Medium – wie beispielsweise Luft – bewegen, ist diese Frequenzänderung unterschiedlich groß. Doppler gab in seinem 1842 erschienenen Standardwerk „Ueber das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels“ folgende Formeln für die Berechnung der vom Empfänger wahrgenommenen Frequenzen an.

In diesen Formeln steht
   für die vom Empfänger wahrgenommene Frequenz
   für die vom Sender abgestrahlte Frequenz
   für die Geschwindigkeit des Empfängers relativ zum Medium
   für die Geschwindigkeit des Senders relativ zum Medium und
    für die Ausbreitungsgeschwindigkeit der Welle im Medium (Schallgeschwindigkeit)

Fall 1: Empfänger ruht, Sender bewegt sich: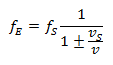

Fall 2: Sender ruht, Empfänger bewegt sich: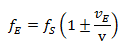

Diese beiden Gleichungen beschreiben den klassischen Doppler-Effekt. Die Wirkung der Frequenzänderung hängt demnach davon ab, mit welcher Geschwindigkeit sich Sender und Empfänger relativ zum Ausbreitungsmedium der Welle bewegen. Das war eine zu Dopplers Zeiten revolutionäre Erkenntnis. Doppler schreibt in seiner Originalarbeit: „Von diesen rein subjectiven Bestimmungen, nicht aber von dem objectiven Sachverhalte hängt die Farbe und Intensität einer Lichtempfindung oder die Tonhöhe und Stärke irgend eines Schalls ab.“

Der Doppler-Effekt und das Licht

Christian Doppler ging davon aus, dass dieser Effekt für jegliche Art von Wellen gelte. Die damalige Annahme der Wissenschaft war, dass auch Licht ein Ausbreitunsmedium benötige, dessen Beschaffenheit allerdings nicht bekannt war und als „Äther“ bezeichnet wurde. Erst 1881 beziehungsweise 1887 konnten die Physiker Albert A. Michelson und Edward W. Morley experimentell nachweisen, dass ein solcher Äther als Ausbreitungsmedium für Licht nicht existiert (Michelson-Morley-Experiment). Heute weiß man, dass der klassische Doppler-Effekt nur für Wellen gültig ist, die sich in einem Medium ausbreiten.

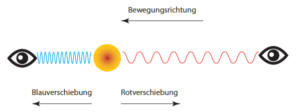
Ein Doppler-Effekt tritt aber dennoch auch für elektromagnetische Wellen wie Licht auf, welche kein Trägermedium benötigen. Daraus ergibt sich auch die Farbverschiebung – nach Blau, wenn sich der Sender dem Empfänger nähert und die Wellen „gequetscht“ werden, und im umgekehrten Fall nach Rot, weil die Wellen „gestreckt“ werden (siehe Abbildung).

Bei elektromagnetischen Wellen hängt dieser Effekt aber nicht von der Relativbewegung zwischen Trägermedium und Empfänger bzw. Sender ab, sondern nur von der Relativbewegung zwischen Empfänger und Sender. Der Doppler-Effekt für Lichtwellen wird aus diesem Grund als relativistischer Doppler-Effekt bezeichnet. für elektromagnetische Wellen steht die empfangene Frequenz mit der gesendeten Frequenz in folgendem Zusammenhang:

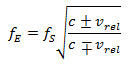
In dieser Formel für den relativistischen Doppler-Effekt bezeichnet c die Lichtgeschwindigkeit mit 299 792 km/s und die Relativgeschwindigkeit zwischen Sender und Empfänger.

Praktische Anwendung der Doppler-Formel

In den folgenden Beispielen werden zwei Spezialfälle für die Ausbreitung einer Schallwelle in Luft betrachtet, wobei die oben erläuterten Variablen für die entsprechenden Frequenzen und Geschwindigkeiten in die Doppler-Formel eingestezt werden.

Fall 1: Der Empfänger ruht relativ zur Luft, der Sender (Schallquelle) bewegt sich mit der Geschwindigkeit zum Empfänger hin (-) oder vom Empfänger weg (+).

Die Doppler-Formel lautet hier:

Ein Beispiel: Ein Autofahrer (Sender der Schallwelle) fährt mit 130 km/h (~36 m/s) an einem am Straßenrand stehenden Fußgänger (Empfänger der Schallwellen) vorbei. Da sich Autofahrer und Fußgänger gut kennen, grüßt der Autofahrer den Fußgänger mit einem langen Hupton. Die Tonhöhe des Huptons beträgt 1 000 Hertz. Welche Tonhöhe nimmt der Fußgänger wahr?

Der Fußgänger hört bei der Annäherung des Autos eine Tonhöhe mit einer Frequenz von:

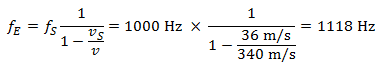
Entfernt sich das Auto vom Empfänger, fällt die Tonhöhe aber ab:

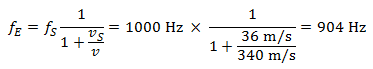
Somit steigt beim Herannahen des Autos die Tonhöhe um 118 Hertz an und fällt bei dessen Entfernung vom Fußgänger um 96 Hertz ab. 1 000 Hertz entsprechen als Ton ungefähr dem „hohen C“, das zwei Stufen über dem System der fünf Notenlinien steht. Die Veränderungen der Tonhöhe beim Herannahen und Weiterfahren des Autos sind in diesem Fall geringfügig unterschiedlich und betragen rund einen Halbton.

Fall 2: Der Sender (Schallquelle) ruht relativ zur Luft, der Empfänger bewegt sich mit der Geschwindigkeit zum Sender hin (+) oder vom Sender weg (-).

Die Doppler-Formel lautet hier:

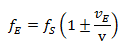
Ein Beispiel: Der Autofahrer ist nun der Empfänger und fährt mit 130 km/h (~36 m/s) an dem am Straßenrand stehenden Bekannten (Sender) vorbei. Zufällig hat dieser eine Hupe bei sich und begrüßt den Vorüberfahrenden mit einem langen Hupton der Tonhöhe 1000 Hertz.

Der Autofahrer hört bei der Annäherung einen Ton mit einer Frequenz von:

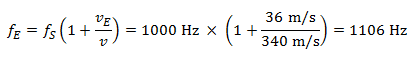
Bei einer Entfernung vom Fußgänger weg hört er einen Ton mit einer Frequenz von:

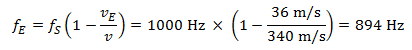
In diesem Fall ist die vom Empfänger (Autofahrer) wahrgenommene Änderung der Tonhöhe bei Annäherung und Entfernung des Autos vom hupenden Bekannten gleich, nämlich jeweils 106 Hertz.

Die Ursache für den Unterschied der Frequenzänderungen in diesen beiden Fällen ist, dass Schall ein Ausbreitungsmedium benötigt. Das ist in diesen Beispielen die Umgebungsluft. In Fall 1 bewegt sich der Sender (die Schallquelle) relativ zur Luft, in Fall 2 der Empfänger.

Basierend auf dem Buch:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Verlag Anton Pustet 2017

Ein weiterer Blick auf den Doppler-Effekt

Jeder kennt den Doppler-Effekt !  Wirklich ?

Mehr als 150 Jahre bevor Christian Doppler den nach ihm benannten Effekt beschrieb und ihn in Formeln fasste, bestimmten O. Rømer und seine Kollegen damit die Lichtgeschwindigkeit.

Es ist physikalisches Allgemeinwissen, dass der Doppler Effekt Frequenzänderungen von Wellen beschreibt, wenn sich Sender und Empfänger der Welle gegeneinander bewegen. Das Ergebnis der Beobachtung ist also die Beschreibung eines kinematischen Phänomens.

Braucht es dazu unbedingt eine Welle als Kommunikationsmittel zwischen Sender und Empfänger? Nein; es geht auch anders und zwar mit dem „Leuchtturm Doppler-Effekt“. Auf einem Leuchtturm dreht sich ein Scheinwerfer mit fester Umlaufgeschwindigkeit. Ein stationärer Beobachter in einiger Entfernung sieht dann mit regelmäßiger Frequenz einen kurzen Lichtpuls. Nähert oder entfernt sich der Beobachter vom Leuchtturm, so wird sich die Empfangsfrequenz des Lichtpulses erhöhen oder vermindern – genauso wie beim „klassischen“ Doppler Effekt die Frequenz der Welle. In der Praxis wird dies kaum auffallen, da sich die Beobachter (z.B. Schiffe) nur langsam bewegen.

Wie schon oben erwähnt, wird dieser „Leuchtturm Doppler-Effekt“ aber in der Astronomie seit langem benutzt. Hier ist das erste, etwas ungewöhnliche Beispiel: Zu Rømers Zeit, d.h. am Ende des 17. Jahrhunderts, waren mit Hilfe der Kepler-Gesetze die Umlaufgeschwindigkeiten der Planeten um die Sonne und damit auch die relativen Entfernungen und Geschwindigkeiten der Planeten zueinander gut bekannt. Galilei hatte die vier größeren Jupiter-Monde entdeckt. Im Besonderen konnte die Umlaufzeit von Io, des innersten dieser vier Monde, durch das regelmäßige Verschwinden oder Auftauchen hinter Jupiter gemessen werden.¹ Nach einigen Jahren genauer Beobachtung stellte sich jedoch heraus, dass diese Umlaufgeschwindigkeit während eines Jahres schwankte ! Da aber die Newton-Mechanik außer Zweifel stand, brauchte es eine andere Erklärung dieses Phänomens.

Rømer hatte nun die gloriose Idee, dass das Licht, das ja das Verschwinden oder Auftauchen von Io („das Signal“) vermittelt, eine endliche Geschwindigkeit haben könnte und das Phänomen durch die bekannte Geschwindigkeit der Erde relativ zu Jupiter erklärt werden könnte, die sich ja während eines Jahres ändert. Die Erde ist näher an der Sonne und dreht sich daher rascher um sie als Jupiter. In bestimmten Zeiten nähert sich die Erde Jupiter, später entfernt sie sich wieder von ihm. Die Beobachtungen von Io unterliegen dem Leuchtturm Effekt ! Die erste Bestimmung der Lichtgeschwindigkeit war zwar nicht sehr genau, aber von der richtigen Größenordnung, was manche damalige Physiker schockierte.

Ein zweites Beispiel aus neuerer Zeit ist ebenfalls sehr beeindruckend. Der Pulsar PSR1913+16 dreht sich 17 Mal pro Sekunde um sich selbst und sendet dabei Radioimpulse in einem wohldefinierten Kegel aus. Wenn dieser Kegel die Erde kreuzt, so empfangen unsere Radioteleskope einen wenige Millisekunden dauernden Radiopuls. Wäre der (etwa 22000 Lichtjahre entfernte) Pulsar stationär, so würde die Frequenz der Pulse nur im Takt des Umlaufs der Erde um die Sonne variieren. Die Variation der Empfangszeiten der Pulse und die Variation ihrer Frequenz ist aber wesentlich rascher, größer und häufiger.

Was die Physiker am Ende des 17. Jahrhunderts leisteten, wiederholten R. Hulse und J. Taylor in der zweiten Hälfte des 20. Jahrhunderts. Sie konnten die Ankunftszeiten der Pulse und deren Schwankungen damit erklären, dass PSR1913+16 mit einem anderen Neutronenstern ein Binärsystem bildet und dass sich die beiden Sterne mit großer Geschwindigkeit elliptisch um ihren gemeinsamen Schwerpunkt drehen, wobei ein voller Umlauf nur 7,75 Stunden dauert.² Die Bahngeschwindigkeit der beiden Sterne ist dabei im Punkt ihrer größten Nähe viermal höher als im Punkt größter Entfernung – ideal für eine Beobachtung durch die Änderung der Intervalle zwischen den Radiopulsen, die das „Leuchtfeuer“ für diesen Doppler Effekt darstellen. Die Messungen sind inzwischen so genau, dass das Binärsystem ein Testobjekt für die Effekte der Allgemeinen Relativitätstheorie darstellt, darunter die rasche Präzession der Umlaufbahnen und die Verminderung der Bahnparameter des Pulsars durch die Abstrahlung von Gravitationswellen. Mit Recht erhielten Hulse und Taylor für ihre Messungen und deren Interpretation 1993 den Nobelpreis für Physik. Inzwischen half diese super-präzise Uhr der Radiopulse die Geschwindigkeit der Bewegung der Sonne um das Zentrum unserer Milchstraße genauer zu vermessen.

Auf einen ersten Blick hin mag der Unterschied zwischen einem „klassischen“ und einem „Leuchtturm“ Doppler-Effekt nicht offensichtlich sein. Dass beim Leuchtturm Effekt in den meisten Fällen das Signal auch durch eine elektromagnetische Welle geliefert wird (sichtbares Licht von Io, ein Breitband-Radiosignal von PSR1913+16), mag zur Verwirrung beitragen. Was aber beim Leuchtturm Effekt gemessen wird, ist nicht die (auf Grund des breiten Spektrums des Lichts oder der Radiowellen praktisch unmessbare) Frequenzänderung der Strahlung, sondern die genaue Ankunftszeit der Signale (Pulse). Um aussagekräftig zu sein, muss die Pulsdauer wesentlich kürzer sein, als das Zeitintervall zwischen aufeinander folgenden Signalen. (Dies ist in den beiden oben beschriebenen Beispielen der Fall.) Wenn sich ein Beobachter mit fixer Geschwindigkeit einem Leuchtturm nähert (oder der Signalgeber dem Beobachter), so werden die Intervalle zwischen zwei aufeinanderfolgenden Signalen kürzer sein, als wenn er sich in Ruhe befindet, da ja das Licht dann zwischen zwei Signalen kürzere Distanzen zurücklegt.

Die Astronomen bezeichnen diese Variationen der Intervalle zwischen aufeinander folgenden Signalen in Abhängigkeit von den Relativgeschwindigkeiten von Sender und Empfänger seit langer Zeit ungeniert als „Doppler-Effekt“. Manche Physiker zögern, weil sie meinen, dass man nur Frequenzänderungen von Wellen als „Doppler- Effekt“ bezeichnen dürfe. Ein Streit um Definitionen ist aber müßig. Da der Endzweck die Messung von Relativgeschwindigkeiten zwischen Sender und Empfänger ist, ist es irrelevant, ob dafür die Veränderung der Frequenz einer Welle („klassischer“ Doppler-Effekt) oder der zeitlichen Intervalle sukzessiver Signalpulse („Leuchtturm-Effekt“) gemessen wird. Die Bezeichnung „Doppler-Effekt“ ist wohl für beide passend, auch wenn Doppler selbst noch nicht an diese Verallgemeinerung dachte. In seiner Originalveröffentlichung von 1842 sprach Doppler aber selbst von „Wellenschlägen“ und leitete aus dem Unterschied der Schlagzahlen pro Zeiteinheit bei Sender und Empfänger die Formeln für den Dopplereffekt ab. Die Formeln gelten daher für beliebige Quellen von „Schlagzahlen“, also auch für „Leuchtturm“-Signale.

Weiterführende Informationen zum Doppler-Effekt | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
² https://de.wikipedia.org/wiki/PSR_J1915%2B1606