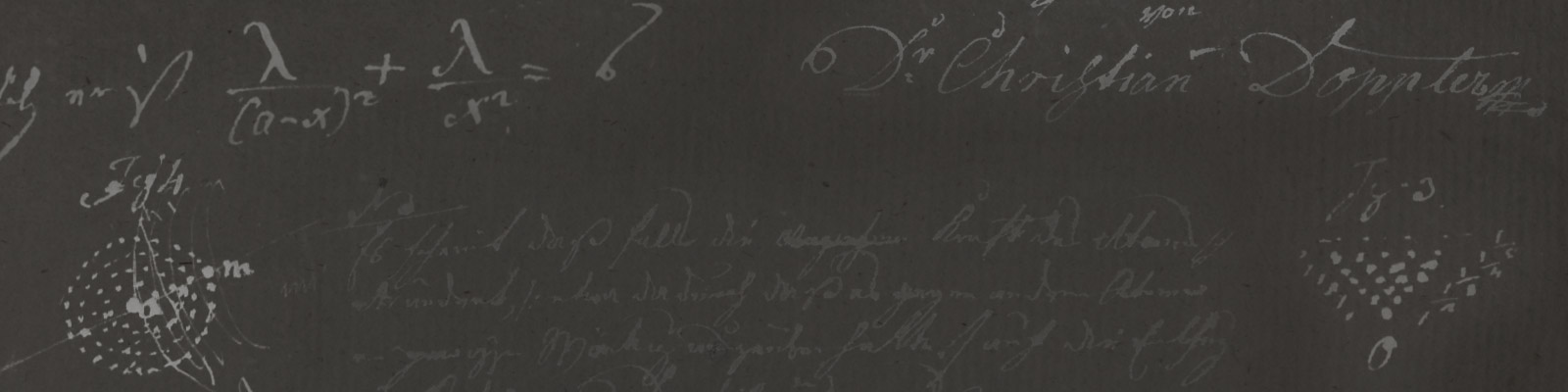From 1796, Bolzano studied philosophy, theology and mathematics in Prague, which influenced him so much as a philosopher that he used to say: “A weak mathematician will never become a strong philosopher”. Ordained as a priest in 1805 and awarded his doctorate, he became professor of religious studies at the university in Prague two days later, initially provisionally and then permanently from 1807. This was linked to the obligation to give “edification speeches” to the university students on Sundays and public holidays. He summarised these in three maxims: “Promote the common good”; “To be happy and to make happy, that is our destiny” and “I should progress”. The success was so great that it reached as far as Vienna. The result was a decree of dismissal. It was only thanks to the efforts of Archbishop Prince Salm-Salm and other friends that he was left in peace until 1819. Bolzano strove for a rational understanding of Catholicism and social reforms. However, because his influence on the elites and students in Prague grew from year to year and due to alleged heresies (as “he publicly and in a sacred place presented principles that jeopardised the peace of the state”), he was removed from office in 1819, placed under police surveillance and his works were placed on the Index. Bolzano only escaped the consequences of the so-called Bolzano trial, which lasted until 1825, by proving himself intellectually superior to his judges, as well as by his high human reputation, and by living in secret with his friend J. Hoffmann in Techobuz from 1823 to 1841. Later he was financially supported by Count Leo Thun. Since 1815 member of the k. Böhm. Society of Sciences. Strong influence on Franz Brentano and E. Husserl. Counted by the latter as one of the “greatest logicians of all time”.
It was probably Bolzano who, among mathematicians at the beginning of the nineteenth century, posed the most profound questions concerning the foundations of calculus. “If Bolzano had given nothing more to mathematics than his definition of the continuous function,” writes Coolidge, “this alone would secure him a place in the history of the discipline.” Bolzano’s “Theory of Functions” was later found in his estate and first published in Prague in 1930.
Bernard Bolzano and Christian Doppler
When Doppler came to Prague in 1835, Bolzano, who was described in a Czech encyclopaedia as “one of the most excellent and perfect men of his time”, was still in Techobuz. We know, however, that he referred to Franz Exner Doppler as a “friend” in a letter dated 19 October 1837. Bolzano was fascinated by this physicist’s speculative method, which was quite unusual in physics at the time and seemed similar to his thinking in mathematics. As he wrote in a letter to Fesl on 24 July 1842, he “yearned” for a young scholar who, while he was still alive, would familiarise himself with his concepts under his guidance and then take it upon himself to write the work. So he was pleased when he learnt in Techobuz that Doppler had already received his first lecture at a meeting of the mathematical section of the Imperial Bohemian Academy of Sciences. Akad. d. Wiss. on 3 December 1840, Doppler made critical remarks about Kulik’s essay on the parallelogram of forces. Despite Kulik’s resistance, he managed to get Doppler’s first essay in Prague included in the publications of the Royal Bohemian Academy and, after the latter presented his principle on 25 May 1842, he supported Doppler uncompromisingly. Like Kreil, he published a theoretical paper on the subject in the year of the discovery, emphasising that Doppler’s work did more than the title promised and was equally important for acoustics and optics, as for wave theory as a whole.
Doppler became Bolzano’s only mathematical dialogue partner at the Academy. It is remarkable that on 5 November 1846, Doppler was the only listener (with the exception of the meteorologist Fritsch) to whom Bolzano presented his theory of functions, which later became so famous and laid the foundation for modern analysis by clarifying the concept of the “continuous function”. Nevertheless, it is surprising that Doppler’s encounter with Bolzano has never been documented to this day. The works of both suffered a similar fate for almost an entire century. Doppler’s mathematical works, with the exception of the brief statement by Prof. Edmund Hlawka (see Peter Schuster, Christian Doppler (1803-1853), 2nd volume, 3rd part, das Werk, Böhlau, 1992) have remained unappreciated to this day.
Bolzano appreciates Doppler. However, he is also the first to recognize that Doppler’s path as a physicist is different, and he accepts this. He writes a detailed appraisal of Doppler’s experimental work and summarizes: “And so all physicists and astronomers would now have plenty to do! Anyone who has the leisure would be offered the opportunity for very meritorious work, for experiments and observations which, whatever they may turn out to be, promote science and should therefore also receive grateful recognition”.
Bolzano endeavors to find Doppler, whose lung disease makes itself drastically felt in 1845, another post. He thought he should give up his professorship and accept a position in the science administration or with a rich aristocrat. He floated the idea of offering Doppler a post in the course of founding the Academy in Vienna. In fact, Doppler’s state of health already resembled a catastrophe. In the months from January to June 1846, he presented the incredible number of eleven scientific papers at the meetings of the Ges. der Wissenschaften. Bolzano was worried about his friend and wrote to Fesl on February 7, 1846: “Professor Doppler has been exciting me for several weeks with one outstanding idea after another and literally keeps me busy day and night. It is incredible what creative genius Austria has in this scholar”. He asks whether the treatise on Doppler by Kreil has already come into the hands of the people “on whom it depends whether such a genius will be saved for science or perish as Pegasus under the yoke. For the worst is to be feared”.
When Bolzano read out his treatise on the “Paradoxes of Mathematics” and the “Paradoxes of Infinity” on February 24, 1848 and then on November 30, 1848 at his last meeting in the Section for Philosophy and Pure Mathematics before his death on December 18, 1848, there was not a single mathematician in the audience. Doppler has already gone his own way. Doppler is in Schemnitz.
Dr. Peter Maria Schuster, 2017