The Doppler Effect

The physics of the Doppler Effect.

The Doppler effect describes how the frequency of a wave changes according to how the emitter or receiver of the wave is moving The classical example used to explain the Doppler effect is that of an ambulance driving past an observer. The movement of the ambulance causes the sound waves in front of the ambulance to become compressed, and those behind it to be stretched. The observer perceives this effect as a change in the pitch of the siren. As the ambulance travels towards the observer, the pitch is higher. As soon as the ambulance starts to move away, the pitch becomes lower.

This change in wave frequency is greater or smaller depending on whether the signal emitter and / or receiver is moving in a given medium – for example, in air. In his 1842 publication “On the coloured light of binary stars and other stars of the heavens”, Doppler provided the following formula for calculating the frequency perceived by an observer.

This formula includes
   the frequency perceived by the receiver
   the frequency given out by its emitter
   the speed of the receiver relative to the medium in which it is situated
   the speed of the emitter relevant to the medium in which it is situated
  the propagation speed of the wave in its medium (wave speed)

Situation 1: The receiver is stationary, the emitter is moving: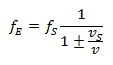

Situation 2: The emitter is stationary, the receiver is moving: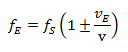

These two equations describe the classical Doppler effect. How the frequency changes thus depends upon the speed with which emitter and receiver are travelling relative to the transmission medium of the wave. This represented a revolutionary finding in Doppler’s time. Thus Doppler writes in his original work: “It is from these purely subjective conditions, and not from objective facts, that the perception of colour and intensity of light, or pitch and strength of a wave depends.”

Light and the Doppler effect

Christian Doppler speculated that this effect was valid for all types of wave. The scientific understanding at the time was that light required a transmission medium. The qualities of this medium were unknown, and it was referred to as “the ether”. It was only in 1881 and 1887 that the physicists Albert A. Michelson and Edward W. Morley were able to prove by experiment that there was no such ether that acted as a transmission medium for light (the Michelson-Morley experiment). Today we know that the classical Doppler effect only applies to waves that propagate within a medium.

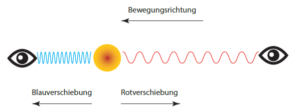
There is, however, also a Doppler effect for electromagnetic waves like light, which do not require a transmission medium. This is at the origin of colour shifts – towards blue when the emitter is moving towards the receiver and the waves are “squashed”, and towards red when the emitter is moving away, and the waves become “stretched” (see diagram).

In the case of electromagnetism, this effect is not dependent on the relative movement between the transmission medium and the receiver or emitter, but on the relative movement between receiver and emitter. For this reason, the Doppler effect for light waves is referred to as the relativistic Doppler effect. In the case of electromagnetic waves, the received frequency and the emitted frequency are given as follows:

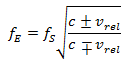
In this formula for the relativistic Doppler effect, c represents the speed of light, at 299 792 km/s, and the relative speed of movement between emitter and receiver.

Practical applications of the Doppler formula

The following examples present two special cases of the propagation of a sound wave in air, where the frequency and speed of the movement variables explained above are plugged into the formula.

Situation 1: The receiver is stationary relative to the air, the emitter (source of the sound wave) is moving towards the receiver (-) or away from the receiver (+).

In this case the Doppler formula is:

For example: a car (sound wave emitter) travels at 130 km/h (~36 m/s) past a pedestrian standing at the side of the road (sound wave receiver). The driver and the pedestrian know each other, so the driver greets the pedestrian with a long honk on the horn. The pitch of the horn is 1 000 Hertz. What pitch does the pedestrian perceive?

As the car is approaching, the pedestrian hears a frequency of:

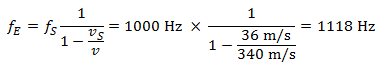
When the car moves away from the receiver, the pitch drops to:

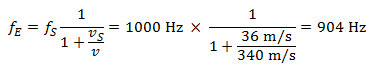
In this way, as the car approaches, the pitch rises by 118 Hertz and then drops by 96 Hertz as the car moves away from the pedestrian. 1 000 Hertz corresponds to “high C”, the note found two lines above the typical five-line musical stave.  In this example, the changes in pitch during the car’s approach and as it moves away are small, and represent only about one semi-tone.

Situation 2: The emitter (source of the sound wave) is stationary relative to the air and the receiver is moving towards the emitter (+) or away from the emitter (-).

In this case the Doppler formula is:

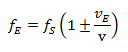
For example: the car driver is now the receiver, and travels past their acquaintance standing at the roadside at 130 km/h (~36 m/s). By chance, the pedestrian has a horn with him, and greets the car driver with a long honk of the horn at a frequency of 1000 Hertz.

Approaching the pedestrian, the driver hears a note with a frequency of:

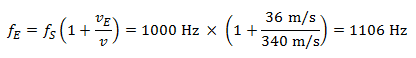
Moving away from the pedestrian, the driver hears a note with a frequency of:

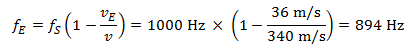
In this scenario, the change in pitch perceived by the receiver (the driver) as they approach and move away from their acquaintance with the horn is the same, i.e. it goes up and down by 106 Hertz.

The reason for the difference in the changes in frequency in these two scenarios is that waves require a transmission medium, which in these cases is the air. In the first scenario, the emitter (the source of the soundwave) moves relative to the air, whereas in the second scenario it is the receiver who moves.

Based on the book:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Verlag Anton Pustet 2017

Another View on the Doppler Effect

Everybody knows the Doppler effect!   Really?

More than 150 years before Christian Doppler described and mathematically formulated the effect named after him the Danish astronomer Ole Rømer and his colleagues used the phenomenon to measure the speed of light.

Basic textbook physics holds that the Doppler effect involves a shift of frequencies when the emitter and receiver of a wave move with respect to one another. This kinematic phenomenon generates information about their relative motion.

But do we actually need waves to communicate between the source and the observer? No. Consider a lighthouse beacon which rotates at fixed frequency and emits an intense parallel beam of light. A stationary observer at some distance will see light pulses at regular intervals. If, however, the receiver approaches or recedes from the lighthouse, the frequency of the light pulses received will increase or decrease – exactly as the frequency of a light wave described by the “classic” Doppler effect. The targets for lighthouse beacons are vessels which move quite slowly, so the effect will hardly be discernable in this context. In astronomy, however, the effect has been useful for centuries…

In the late 17^th century the orbital speeds of the planets around the sun were known via Kepler’s laws. As a consequence, the distances and speeds of the planets relative to each other were already well established.

Galileo had discovered the four big moons of Jupiter. The time it took Io, the innermost of the four moons, to complete a full orbit could be measured by its disappearance or re-emergence from behind Jupiter. After some years of precise observations these measurements indicated a variation of Io’s rotational speed which curiously changed over the year! As Kepler’s laws were well established, another explanation for this strange observation had to be found.

Ole Rømer’s glorious idea was that light which came from the moon Io might be travelling at a fixed speed: the observed variations of Io’s orbital speed might be caused by the speed of earth relative to Jupiter¹ which is changing over the year. Earth is closer to the sun than Jupiter and so rotates faster around the sun than Jupiter. At certain times the earth is approaching Jupiter, at other times it is receding. So, the observations of Io are subject to the lighthouse effect. This allowed Rømer’s colleagues to measure the speed of light, albeit imprecisely but impressively within the correct order of magnitude. The enormous speed of light shocked quite a number of physicists of the day.

A more recent example can be found in contemporary astronomy. The pulsar PSR1913+16 is a neutron star which rotates around itself 17 times per second. As its magnetic field is not aligned with the axis of rotation the pulsar emits radio waves within a well-defined cone. When these waves hit the earth with the frequency of the pulsar’s rotation, radio telescopes receive an intense short pulse lasting some milliseconds. If this pulsar (at a distance of about 22000 lightyears from the sun) were stationary, the frequency of the pulses received would only vary with the earth’s rotation around the sun. However, the pulses received vary much faster and the variations are much bigger than expected.

What the astronomers at the end of the 17th century achieved Russel Hulse and Joseph Taylor repeated during the second half of the 20th century. They explained the variations of the arrival times of the radio pulses from PSR1913+16 with the hypothesis that this pulsar forms a binary system with another neutron star. The two stars rotate around their common centre of gravity in elliptical trajectories in only 7.75 hours.² At their point of closest approach their speed is four times bigger than the speed at their biggest distance – ideal for observations by the variation of the arrival times of the radio pulses which represent the “lighthouse signals“ for this Doppler effect. This binary system has now been observed for 50 years and the measurement are so precise that they represent a “model system“ for the effects described by the General Theory of Relativity, e.g. the relatively rapid precession of the orientation of the elliptical trajectories and their „shrinking“, i.e. the loss of energy by radiation of gravitational waves. For their measurements and their interpretation Hulse and Taylor were awarded the 1993 Nobel Prize in physics. The radio pulses of PSR1913+16 represent one of the most precise clocks in the universe and help to measure the speed of the sun around the centre of our galaxy more precisely.

On a first look the difference between a “classical” Doppler effect and a “lighthouse” effect may not be obvious. What may add to a confusion is that in the lighthouse effect the signal is transported by an electromagnetic wave (visible light by Io or the broad band radio signal from PSR1913+16). However, what is measured by the lighthouse effect is not the (almost unmeasurable) variation of the frequency of this radiation but the exact arrival times of the signals. For that to be meaningful the pulse duration of the signals has to be much shorter than the interval between the pulses. (This is the case in the two examples presented above.) If an observer approaches a lighthouse with fixed speed the intervals between two successive pulses will be shorter than in the stationary case as the light has to travel ever shorter distances between two successive observations.

Astronomers freely use the term “Doppler effect” when referring to time variations of signals depending on the relative motion of emitter and receiver. Some physicists balk at this usage because they consider the effect to be limited to frequency variations of waves. However, quarreling about definitions is not productive. The purpose of the measurements is always the determination of the relative speed of the emitter with respect to the receiver, so it is irrelevant if a wave or a lighthouse signal is used. Both techniques are worthy of being called a “Doppler effect“, even if Doppler himself may not have imagined this more general application. In his original paper presented in 1842 Doppler himself talked of „beats“ and he derived the formulae for the effect named after him by the difference of beats of the emitter and the ones experienced by the receiver. Therefore, the formulae are valid for any kind of „beats“ including the ones of the lighthouse type.

Further information on the Doppler effect | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
² https://de.wikipedia.org/wiki/PSR_J1915%2B1606