El efecto Doppler

La física del efecto Doppler

El efecto Doppler describe cómo cambia la frecuencia de una onda en función del movimiento del emisor o del receptor de la misma. El ejemplo clásico utilizado para explicar el efecto Doppler es el de una ambulancia que pasa por delante de un observador. El movimiento de la ambulancia hace que las ondas sonoras delante de ella se compriman y las de detrás se estiren. El observador percibe este efecto como un cambio en el tono de la sirena. A medida que la ambulancia se acerca al observador, el tono es más alto. En cuanto la ambulancia empieza a alejarse, el tono se vuelve más bajo.

Este cambio en la frecuencia de la onda es mayor o menor dependiendo de si el emisor y/o el receptor de la señal se mueven en un medio determinado, por ejemplo, en el aire. En su publicación de 1842 «Sobre la luz coloreada de las estrellas binarias y otros astros del cielo», Doppler proporcionó la siguiente fórmula para calcular la frecuencia percibida por un observador.

Esta fórmula incluye
   la frecuencia percibida por el receptor
   la frecuencia emitida por su emisor
  la velocidad del receptor en relación con el medio en el que se encuentra
   la velocidad del emisor en relación al medio en el que se encuentra
   la velocidad de propagación de la onda en su medio (velocidad de onda)

Situación 1: El receptor está estacionario, el emisor se mueve: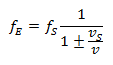

Situación 2: El emisor está estacionario, el receptor se mueve: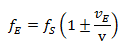

Estas dos ecuaciones describen el efecto Doppler clásico. La variación de la frecuencia depende, pues, de la velocidad a la que se desplazan el emisor y el receptor en relación con el medio de transmisión de la onda. Esto representó un hallazgo revolucionario en la época de Doppler. Así, Doppler escribe en su obra original «De estas condiciones puramente subjetivas, y no de hechos objetivos, depende la percepción del color y la intensidad de la luz, o el tono y la fuerza de una onda».

La luz y el efecto Doppler

Christian Doppler especuló que este efecto era válido para todos los tipos de ondas. En esa época, los científicos creían que la luz necesitaba un medio de transmisión. Las cualidades de este medio eran desconocidas y se le denominaba «el éter». No fue hasta 1881 y 1887 que los físicos Albert A. Michelson y Edward W. Morley pudieron demostrar experimentalmente que no existía un éter que actuara como medio de transmisión de la luz (el experimento de Michelson-Morley). Hoy sabemos que el efecto Doppler clásico sólo se aplica a las ondas que se propagan dentro de un medio.

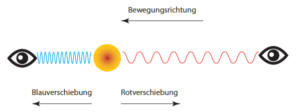
Sin embargo, también existe un efecto Doppler para las ondas electromagnéticas como la luz, que no necesitan un medio de transmisión. Esto es el origen de los cambios de color: hacia el azul cuando el emisor se acerca al receptor y las ondas se «aplastan», y hacia el rojo cuando el emisor se aleja y las ondas se «estiran» (ver diagrama).

En el caso del electromagnetismo, este efecto no depende del movimiento relativo entre el medio de transmisión y el receptor o el emisor, sino del movimiento relativo entre el receptor y el emisor. Por esta razón, el efecto Doppler para las ondas luminosas se denomina efecto Doppler relativista. En el caso de las ondas electromagnéticas, la frecuencia recibida y la frecuencia emitida vienen dadas por:

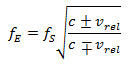
En esta fórmula del efecto Doppler relativista, c representa la velocidad de la luz, a 299 792 km/s, y la velocidad de movimiento relativo entre el emisor y el receptor..

Aplicaciones prácticas de la fórmula Doppler

Los siguientes ejemplos presentan dos casos especiales de propagación de una onda sonora en el aire, donde la frecuencia y la velocidad de las variables de movimiento explicadas anteriormente se introducen en la fórmula.

Situación 1: El receptor está estacionario en relación con el aire, el emisor (fuente de la onda sonora) se mueve hacia el receptor (-) o se aleja del receptor (+).

En este caso la fórmula Doppler es:

Por ejemplo: un coche (el emisor de las ondas sonoras) pasa a 130 km/h (~36 m/s) junto a un peatón que está parado al lado de la carretera (el receptor de las ondas sonoras). El conductor y el peatón se conocen, por lo que el conductor saluda al peatón con un toque largo de bocina. El tono de la bocina es de 1.000 hercios. ¿Qué tono percibe el peatón?

Cuando el coche se acerca, el peatón escucha una frecuencia de:

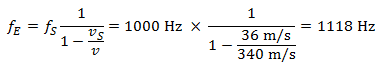
Cuando el coche se aleja del receptor, el tono baja a:

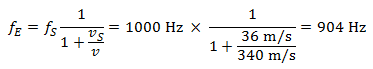
Así pues, a medida que el coche se acerca, el tono sube 118 hercios y luego baja 96 hercios cuando el coche se aleja del peatón. 1.000 hercios corresponden al «do agudo», la nota que se encuentra dos líneas por encima del pentagrama musical típico de cinco líneas.  En este ejemplo, los cambios de tono durante la aproximación del coche y su alejamiento son pequeños y representan sólo un semitono.

Situación 2: El emisor (la fuente de la onda sonora) está estacionario en relación con el aire y el receptor se mueve hacia el emisor (+) o se aleja del emisor (-).

En este caso la fórmula Doppler es:

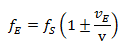
Por ejemplo: el conductor del coche es ahora el receptor, y pasa junto a su conocido parado en el arcén a 130 km/h (~36 m/s). Por casualidad, el peatón tiene una bocina y saluda al conductor del coche con un toque largo de bocina a una frecuencia de 1.000 hercios.

Al acercarse al peatón, el conductor escucha una nota con una frecuencia de:

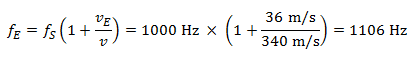
Al alejarse del peatón, el conductor escucha una nota con una frecuencia de:

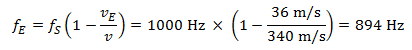
En este escenario, el cambio de tono percibido por el receptor (el conductor) al acercarse y alejarse de su conocido con la bocina es el mismo, es decir, sube y baja 106 hercios.

La razón de la diferencia en los cambios de frecuencia entre estos dos escenarios es que las ondas requieren un medio de transmisión, que en estos casos es el aire. En el primer escenario, el emisor (la fuente de la onda sonora) se mueve con respecto al aire, mientras que en el segundo escenario es el receptor quien se mueve.

Basado en el libro:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Verlag Anton Pustet 2017

El efecto Doppler desde otro punto de vista

 ¡Todo el mundo conoce el efecto Doppler! ¿Es eso verdad?

Más de 150 años antes de que Christian Doppler describiera y formulara matemáticamente el efecto que lleva su nombre, el astrónomo danés Ole Rømer y sus colegas utilizaron este fenómeno para medir la velocidad de la luz.

Según los libros de texto de física básica, el efecto Doppler implica un desplazamiento de las frecuencias cuando el emisor y el receptor de una onda se mueven uno respecto al otro. Este fenómeno cinemático genera información sobre su movimiento relativo.

Pero ¿necesitamos realmente ondas para comunicarnos entre la fuente y el observador? No. Pensemos en un faro que gira a una frecuencia fija y emite un intenso haz paralelo de luz. Un observador inmóvil situado a cierta distancia verá impulsos luminosos a intervalos regulares. Sin embargo, si el receptor se acerca o se aleja del faro, la frecuencia de los impulsos luminosos recibidos aumentará o disminuirá, exactamente igual que la frecuencia de una onda luminosa descrita por el efecto Doppler «clásico». Los objetivos de las balizas de los faros son buques que se mueven con bastante lentitud, por lo que el efecto apenas será perceptible en este contexto. En astronomía, sin embargo, el efecto ha sido útil durante siglos…

A finales del siglo XVII se conocían las velocidades orbitales de los planetas alrededor del Sol gracias a las leyes de Kepler. Por consiguiente, las distancias y velocidades de los planetas entre sí ya estaban bien establecidas.

Galileo había descubierto las cuatro grandes lunas de Júpiter. El tiempo que tardaba Io, la más interna de las cuatro lunas, en completar una órbita podía medirse por su desaparición o reaparición por detrás de Júpiter. Tras algunos años de precisas observaciones, estas mediciones indicaron una variación de la velocidad de rotación de Io que, curiosamente, ¡cambiaba a lo largo del año! Y como las leyes de Kepler estaban bien establecidas, había que encontrar otra explicación para esta extraña observación.

La memorable idea de Ole Rømer fue que la luz procedente de la luna Io podría estar viajando a una velocidad fija: las variaciones observadas en la velocidad orbital de Io podrían estar causadas por la velocidad de la Tierra con respecto a Júpiter¹, que cambia a lo largo del año. La Tierra está más cerca del Sol y, por tanto, gira más rápido alrededor del Sol que Júpiter. En ciertos momentos la Tierra se acerca a Júpiter, en otros se aleja. Así pues, las observaciones de Io están sujetas al efecto faro. Esto permitió a los colegas de Rømer medir la velocidad de la luz, aunque de forma imprecisa pero también impresionante dentro del orden de magnitud correcto. La enorme velocidad de la luz conmocionó a muchos de los físicos de la época.

Un ejemplo más reciente se encuentra en la astronomía contemporánea. El púlsar PSR1913+16 es una estrella de neutrones que gira sobre sí misma 17 veces por segundo. Como su campo magnético no está alineado con el eje de rotación, el púlsar emite ondas de radio dentro de un cono bien definido. Cuando estas ondas inciden en la Tierra con la frecuencia de rotación del púlsar, los radiotelescopios reciben un pulso corto e intenso que dura unos milisegundos. Si este púlsar – que se encuentra a una distancia de unos 22000 años luz del Sol – fuera estacionario, la frecuencia de los pulsos recibidos sólo variaría con la rotación de la Tierra alrededor del Sol. Sin embargo, los pulsos recibidos varían mucho más rápido y las variaciones son mucho mayores de lo esperado.

Lo que los astrónomos de finales del siglo XVII habían logrado, lo repitieron Russel Hulse y Joseph Taylor durante la segunda mitad del siglo XX. Explicaron las variaciones en los tiempos de llegada de los pulsos de radio de PSR1913+16 con la hipótesis de que este púlsar forma un sistema binario con otra estrella de neutrones. Estas dos estrellas giran alrededor de su centro común de gravedad en trayectorias elípticas en sólo 7,75 horas.² En su punto de mayor aproximación, su velocidad es cuatro veces mayor que la velocidad a su mayor distancia – ideal para las observaciones de la variación en los tiempos de llegada de los pulsos de radio, que representan las «señales faro» de este efecto Doppler.

Este sistema binario lleva observándose 50 años y las mediciones son tan precisas que representan un «sistema modelo» para los efectos descritos por la Teoría General de la Relatividad, por ejemplo, la relativamente rápida precesión de la orientación de las trayectorias elípticas y su «encogimiento», es decir, la pérdida de energía por radiación de ondas gravitatorias. Hulse y Taylor recibieron el Premio Nobel de Física en 1993 por estas mediciones y su interpretación. Los pulsos de radio de PSR1913+16 representan uno de los relojes más precisos del universo y ayudan a medir con mayor exactitud la velocidad del Sol alrededor del centro de nuestra galaxia.

A primera vista, la diferencia entre un efecto Doppler «clásico» y un efecto «faro» puede no resultar obvia. Lo que puede provocar la confusión es que en el efecto faro la señal es transportada por una onda electromagnética: la luz visible de Io o la ancha banda de señales de radio de PSR1913+16. Sin embargo, lo que mide el efecto faro no es la variación (casi inconmensurable) de la frecuencia de esta radiación, sino los tiempos exactos de llegada de las señales. Para que esto sea significativo, la duración del pulso de las señales tiene que ser mucho más corta que el intervalo entre los pulsos. Y esto es lo que sucede en los dos ejemplos anteriores. Si un observador se acerca a un faro con una velocidad fija, los intervalos entre dos pulsos sucesivos serán más cortos que en el caso que el observador esté quieto, ya que la luz tiene que recorrer distancias cada vez más cortas entre dos observaciones sucesivas.

Los astrónomos utilizan libremente el término «efecto Doppler» para referirse a las variaciones temporales de las señales en función del movimiento relativo del emisor y el receptor. Algunos físicos se oponen a este uso porque consideran que el efecto se limita a las variaciones de frecuencia de las ondas. Sin embargo, discutir sobre definiciones no es productivo. El objetivo de las mediciones siempre es la determinación de la velocidad relativa del emisor con respecto al receptor, por lo que es irrelevante si se utiliza una señal de onda o de faro. Ambas técnicas son dignas de llamarse «efecto Doppler», aunque el propio Doppler no imaginara esta aplicación más general. En su artículo original, presentado en 1842, el propio Doppler hablaba de «pulsaciones» y derivó las fórmulas del efecto que lleva su nombre por la diferencia entre las “pulsaciones” del emisor y las que experimenta el receptor. Por lo tanto, las fórmulas son válidas para cualquier tipo de «pulsaciones», incluidas las de tipo faro.

Further information on the Doppler effect | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
² https://es.wikipedia.org/wiki/PSR_B1913%2B16