Effet Doppler

La physique de l’effet Doppler

L’effet Doppler décrit le changement de fréquence d’une onde en fonction de l’état de mouvement de son émetteur et/ou de son récepteur. L’exemple classique pour expliquer l’effet Doppler est celui d’une ambulance qui passe devant un observateur. En raison du mouvement de l’ambulance, les ondes sonores sont comprimées devant la voiture et dilatées derrière elle. L’observateur perçoit alors cet effet par la différence de hauteur du son de la sirène : avant que l’ambulance ne l’atteigne, le son est plus aigu, dès que la voiture s’éloigne de lui, le son est plus grave.

Selon que l’émetteur et/ou le récepteur se déplacent dans un milieu – comme l’air – cette variation de fréquence est plus ou moins importante. Dans son ouvrage de référence « Ueber das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels » publié en 1842 (sur la lumière colorée des étoiles doubles et autres astres du ciel), Doppler a donné les formules suivantes pour le calcul des fréquences perçues par le récepteur.

Dans ces formules sont définis
   la fréquence perçue par le récepteur
  la fréquence émis par l‘émetteur
  la vitesse du récepteur relative au milieu
   la vitesse de l’émetteur relative au milieu et
   la vitesse de propagation de l’onde dans ce milieu (vitesse du son)

Cas 1: Le récepteur est au repos, l’émetteur se déplace :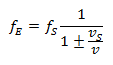

Cas 2: L’émetteur est au repos, le récepteur se déplace :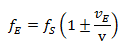

Ces deux équations décrivent l’effet Doppler classique. L’effet du changement de fréquence dépend donc de la vitesse à laquelle l’émetteur et le récepteur se déplacent par rapport au milieu de propagation de l’onde. Il s’agissait d’une découverte révolutionnaire à l’époque de Doppler. Doppler écrit dans son travail original : « C’est de ces déterminations purement subjectives, mais non du fait objectif, que dépendent la couleur et l’intensité d’une sensation lumineuse ou la hauteur et la puissance d’un son quelconque ».

L’effet Doppler et la lumière

Christian Doppler a supposé que cet effet s’appliquait à tous les types d’ondes. L’hypothèse scientifique de l’époque était que la lumière avait également besoin d’un milieu de propagation, dont la nature n’était toutefois pas connue et que l’on appelait « éther ». Ce n’est qu’en 1881 et 1887 que les physiciens Albert A. Michelson et Edward W. Morley ont pu démontrer expérimentalement qu’un tel éther n’existait pas en tant que milieu de propagation de la lumière (expérience de Michelson-Morley). On sait aujourd’hui que l’effet Doppler classique n’est valable que pour les ondes qui se propagent dans un milieu.

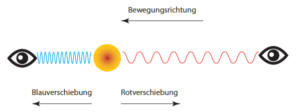
L’effet Doppler se produit néanmoins aussi pour les ondes électromagnétiques comme la lumière, qui n’ont pas besoin d’un support. Il en résulte également un décalage de couleur – vers le bleu lorsque l’émetteur se rapproche du récepteur et que les ondes sont « écrasées », et vers le rouge dans le cas inverse, parce que les ondes sont « étirées » (voir illustration).

Pour les ondes électromagnétiques, cet effet ne dépend toutefois pas du mouvement relatif entre le milieu porteur et le récepteur ou l’émetteur, mais uniquement du mouvement relatif entre le récepteur et l’émetteur. Pour cette raison, l’effet Doppler pour les ondes lumineuses est appelé effet Doppler relativiste. Pour les ondes electromagnétiques la relation entre la fréquence reçue et la fréquence émise s’établit de la manière suivante :

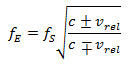
Dans cette formule pour l’effet Doppler relativiste apparait la constante c pour la vitesse de la lumière soit 299 792 km/s et la vitesse relative entre l’émetteur et le récepteur.

Utilisations pratiques des formules Doppler

Dans les exemples suivants, nous considérons deux cas particuliers de propagation d’une onde sonore dans l’air, en utilisant les variables expliquées ci-dessus pour les fréquences et les vitesses correspondantes dans la formule Doppler.

Cas 1 : le récepteur est au repos par rapport à l’air et l’émetteur (source du son) se déplace par rapport au récepteur vers (-) ou depuis (+).

La formule Doppler s’énonce ici :

Exemple : un automobiliste (émetteur des ondes sonores) passe à 130 km/h (~36 m/s) devant un piéton (récepteur des ondes sonores) qui se trouve au bord de la route. Comme l’automobiliste et le piéton se connaissent bien, l’automobiliste salue le piéton d’un long coup de klaxon. La hauteur du son du klaxon est de 1 000 hertz. Quelle est la hauteur du son perçu par le piéton ?

A l’approche de la voiture, le piéton entend un son d’une fréquence de :

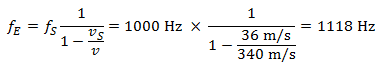
Si la voiture s’éloigne du récepteur, la hauteur du son diminue :

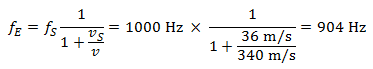
Ainsi, la hauteur du son augmente de 118 hertz à l’approche de la voiture et diminue de 96 hertz lorsque celle-ci s’éloigne du piéton. Le son de 1 000 hertz correspond approximativement au « do aigu », qui se situe deux degrés au-dessus de la portée de cinq notes. Dans ce cas, les changements de hauteur de son à l’approche et à la poursuite du trajet de la voiture sont légèrement différents et représentent environ un demi-ton.

Cas 2 : l’émetteur est au repos par rapport à l’air et le récepteur se déplace à une vitesse  par rapport à l’émetteur vers (+) ou depuis (-).

La formule Doppler s’énonce ici :

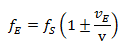
Exemple : l’automobiliste est maintenant le récepteur et passe à 130 km/h (~36 m/s) devant la personne qu’il connaît et qui se trouve au bord de la route (émetteur). Il se trouve que ce dernier a un klaxon sur lui et accueille le passant avec un long son de klaxon d’une hauteur de 1 000 hertz.

Le conducteur entend le son qui se rapproche avec une fréquence de :

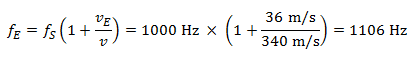
En s’éloignant du piéton il perçoit un son d’une fréquence de :

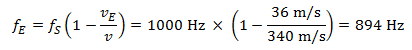
Dans ce cas, la modification de la hauteur du son perçue par le récepteur (l’automobiliste) est la même à l’approche et à l’éloignement de la voiture de la personne connue qui klaxonne, à savoir 106 hertz à chaque fois.

La raison de la différence des changements de fréquence dans ces deux cas est que le son a besoin d’un milieu de propagation. Dans ces exemples, il s’agit de l’air ambiant. Dans le cas 1, l’émetteur (la source sonore) se déplace par rapport à l’air, dans le cas 2, c’est le récepteur.

Basé sur le livre :

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Edition Anton Pustet 2017

Un autre regard sur l’effet Doppler

Tout le monde connaît l’effet Doppler ! Vraiment ?

Plus de 150 ans avant que Christian Doppler ne décrive l’effet qui porte son nom et ne le formule, O. Rømer et ses collègues l’utilisaient pour déterminer la vitesse de la lumière.

Il est de notoriété publique que l’effet Doppler décrit les changements de fréquence des ondes lorsque l’émetteur et le récepteur de l’onde se déplacent l’un par rapport à l’autre. Le résultat de l’observation est donc la description d’un phénomène cinématique.

Faut-il pour cela absolument une onde comme moyen de communication entre l’émetteur et le récepteur ? Non ; il existe une autre façon de procéder, à savoir « l’effet Doppler des phares ». Sur un phare, un projecteur tourne à une vitesse de rotation fixe. Un observateur stationnaire situé à une certaine distance voit alors une courte impulsion lumineuse à une fréquence régulière. Si l’observateur se rapproche ou s’éloigne du phare, la fréquence de réception de l’impulsion lumineuse augmentera ou diminuera – tout comme la fréquence de l’onde dans le cas de l’effet Doppler « classique ». Dans la pratique, cela ne se remarquera guère, car les observateurs (par ex. les bateaux) ne se déplacent que lentement.

Comme nous l’avons déjà mentionné plus haut, cet « effet Doppler du phare » est toutefois utilisé depuis longtemps en astronomie. Voici le premier exemple, un peu inhabituel : à l’époque de Rømer, c’est-à-dire à la fin du XVIIe siècle, les vitesses de rotation des planètes autour du Soleil étaient bien connues à l’aide des lois de Kepler, et donc aussi les distances et vitesses relatives des planètes entre elles. Galilée avait découvert les quatre plus gros satellites de Jupiter. En particulier, la période de rotation de Io, la plus interne de ces quatre lunes, pouvait être mesurée par la disparition ou l’apparition régulière derrière Jupiter.¹ Après quelques années d’observation précise, il s’est toutefois avéré que cette vitesse de rotation variait pendant une année ! Mais comme la mécanique newtonienne ne faisait aucun doute, il fallait trouver une autre explication à ce phénomène.

Rømer eut alors l’idée glorieuse que la lumière, qui transmettait la disparition ou l’apparition de Io (« le signal »), pouvait avoir une vitesse finie et que le phénomène pouvait être expliqué par la vitesse connue de la Terre par rapport à Jupiter, qui varie au cours d’une année. La Terre est plus proche du Soleil et tourne donc plus rapidement autour de lui que Jupiter. À certains moments, la Terre se rapproche de Jupiter, puis s’en éloigne à nouveau. Les observations de Io sont soumises à l’effet de phare ! La première détermination de la vitesse de la lumière n’était certes pas très précise, mais d’un bon ordre de grandeur, ce qui a choqué certains physiciens de l’époque.

Un deuxième exemple plus récent est également très impressionnant. Le pulsar PSR1913+16 tourne sur lui-même 17 fois par seconde en émettant des impulsions radio dans un cône bien défini. Lorsque ce cône croise la Terre, nos radiotélescopes reçoivent une impulsion radio de quelques millisecondes. Si le pulsar (situé à environ 22 000 années-lumière) était stationnaire, la fréquence des impulsions ne varierait qu’au rythme de la rotation de la Terre autour du Soleil. Mais la variation des temps de réception des pulsations et la variation de leur fréquence sont beaucoup plus rapides, plus importantes et plus fréquentes.

Ce que les physiciens ont accompli à la fin du 17e siècle, R. Hulse et J. Taylor l’ont répété dans la seconde moitié du 20e siècle. Ils ont pu expliquer les temps d’arrivée des impulsions et leurs variations par le fait que PSR1913+16 forme un système binaire avec une autre étoile à neutrons et que les deux étoiles tournent à grande vitesse de manière elliptique autour de leur centre de gravité commun, une révolution complète ne durant que 7,75 heures.² La vitesse orbitale des deux étoiles est alors quatre fois plus élevée au point de leur plus grande proximité qu’au point de leur plus grande distance – idéal pour une observation par la modification des intervalles entre les impulsions radio, qui constituent le « phare » de cet effet Doppler. Les mesures sont désormais si précises que le système binaire constitue un objet de test pour les effets de la théorie de la relativité générale, dont la précession rapide des orbites et la réduction des paramètres orbitaux du pulsar par l’émission d’ondes gravitationnelles. C’est à juste titre que Hulse et Taylor ont reçu le prix Nobel de physique en 1993 pour leurs mesures et leur interprétation. Entre-temps, cette horloge super-précise des impulsions radio a aidé à mesurer plus précisément la vitesse du mouvement du Soleil autour du centre de notre Voie lactée.

A première vue, la différence entre un effet Doppler « classique » et un effet Doppler « phare » peut ne pas être évidente. Le fait que, dans la plupart des cas, le signal de l’effet phare soit également fourni par une onde électromagnétique (lumière visible de Io, signal radio à large bande de PSR1913+16) peut contribuer à la confusion. Mais ce qui est mesuré dans l’effet phare, ce n’est pas le changement de fréquence du rayonnement électromagnétique (pratiquement impossible à mesurer en raison du large spectre de la lumière ou des ondes radio), mais le temps exact d’arrivée des signaux (impulsions). Pour être significative, la durée de l’impulsion doit être beaucoup plus courte que l’intervalle de temps entre les signaux successifs. (Si un observateur s’approche d’un phare à une vitesse fixe (ou si l’émetteur du signal s’approche de l’observateur), l’intervalle entre deux signaux successifs sera plus court que si l’observateur est au repos, car la lumière doit alors parcourir des distances plus courtes entre deux signaux.

Les astronomes désignent depuis longtemps et sans complexe ces variations d’intervalles entre signaux successifs en fonction des vitesses relatives de l’émetteur et du récepteur sous le nom « d’effet Doppler ». Certains physiciens hésitent, car ils estiment que seules les variations de fréquence des ondes peuvent être qualifiées « d’effet Doppler ». Mais il est inutile de se disputer sur les définitions. L’objectif final étant de mesurer les vitesses relatives entre l’émetteur et le récepteur, il importe peu de savoir si l’on mesure pour cela la variation de la fréquence d’une onde (effet Doppler « classique ») ou les intervalles de temps des impulsions successives du signal (effet « phare »). Le terme « effet Doppler » convient sans doute aux deux, même si Doppler lui-même ne pensait pas encore à cette généralisation. Dans sa publication originale de 1842, Doppler parlait cependant lui-même de « battements d’ondes » et déduisait les formules de l’effet Doppler de la différence du nombre de battements par unité de temps chez l’émetteur et le récepteur. Les formules sont donc valables pour toutes les sources de « nombres de battements », y compris les signaux « phares ».

Further information on the Doppler effect | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
² https://de.wikipedia.org/wiki/PSR_J1915%2B1606