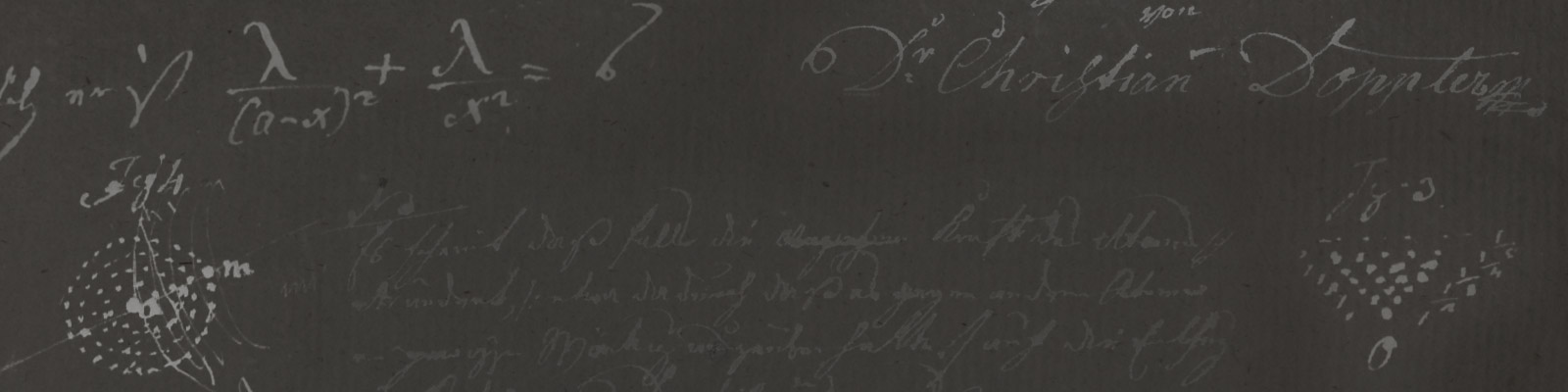Kulik, né à Lemberg (aujourd’hui Lviv), en Galicie, fut nommé professeur de mathématiques au lycée d’Olomouc à l’âge de 21 ans. En 1816, professeur de physique et d’astronomie au lycée de Graz. En 1822, il obtient le titre de docteur et est élu recteur l’année suivante, en 1823. En 1826, il devint professeur de mathématiques supérieures à Prague, où il vécut jusqu’à sa mort. Il dirigea la bibliothèque de la Société royale des sciences de Bohême et réalisa un catalogue de ses fonds jusqu’en 1835.
Kulik appartenait à une génération de mathématiciens plutôt caractéristique du dix-huitième siècle, qui ne se préoccupait pas trop des fondements de leur travail, car dans ce siècle d’expérimentation, « les résultats s’accumulaient à profusion » (Struik, Dirk J. : Abriß der Geschichte der Mathematik, Berlin, 1967, p. 174) – « allez en avant, et la foi vous viendra », aurait dit d’Alembert.
Kulik a créé de vastes tableaux de facteurs et a fondé une méthode de détermination des racines rationnelles à l’aide de tableaux de facteurs. Il y a travaillé sans relâche jusqu’à la fin de sa vie. Il écrit : « Je possède un manuscrit qui contient la suite de la table de Burckard de trois millions à 100 millions sur 4.212 pages in-folio étroitement décrites ». Ses manuscrits (8e volumes) n’ont jamais été consultés et se trouvent dans les archives de l’Académie autrichienne des sciences à Vienne (communication de Mme Dr. Christa Binder, Vienne).
Jakob Kulik et Christian Doppler
Lors de la réunion de la section mathématique du 5 novembre 1840, à laquelle Christian Doppler participe pour la première fois en tant que membre extraordinaire de l’Académie, Kulik lit, en tant que directeur, un article sur une nouvelle preuve analytique du théorème du parallélogramme des forces. Lors de la réunion suivante, le 3 décembre 1840, Christian Doppler fait des remarques critiques sur cet article. Il dit notamment : « Que si la somme des carrés d’une fonction de deux angles qui se complètent pour former une droite est égale à un, il n’en résulte pas que cette fonction soit le cosinus de l’angle, car on peut donner plusieurs fonctions ayant cette propriété et qui sont essentiellement différentes du cosinus ». Kulik rétorqua que « Ref., aurait dépassé les limites imposées à une courte dissertation s’il avait voulu s’attarder plus longtemps sur cette proposition, pour tomber, comme le cite quelque part Littrow, dans l’erreur de certains mathématiciens récents qui « à force de vouloir justifier la chose, ne peuvent pas arriver à la chose elle-même ».
Bolzano, qui apprend cela, vient au secours de Doppler en expliquant dans un travail substantiel qu’on peut tout à fait s’attarder plus longtemps sur les justifications. « Celui qui se contente de la simple certitude qu’une chose est, et qui ne s’interroge pas sur la raison objective pour laquelle elle est, pour lui, bien sûr, le besoin scientifique ne s’est pas encore éveillé du tout ».
Malgré l’opposition de Kulik, Bolzano obtiendra que le premier article de Doppler soit publié à Prague en 1841 dans les écrits de l’Académie royale de Bohême. Elle porte le long titre : « Essai de traitement analytique de lignes, surfaces et corps arbitrairement limités et composés, ainsi qu’une application de celui-ci à divers problèmes de géométrie descriptive et perspective » et a pour but de « généraliser » les doctrines fondamentales de la géométrie analytique.
Kulik, en tant que directeur de la société, émettra également un avis négatif sur la monographie de Doppler en 1843 intitulée : « Versuch einer Erweiterung der analytischen Geometrie auf Grundlage eines neu einzuführenden Algorithmus ». Néanmoins, grâce à l’approbation de Bolzano et Kreil, la publication dans les Abhandl. d. k. Böhm. Ges. d. Wissenschaften V. Folge, 2ème volume, p. 533-700, à Prague en 1843 a bien eu lieu.