L’effetto Doppler

La fisica dell’effetto Doppler

L’effetto Doppler descrive il cambiamento di frequenza di un’onda, a seconda dello stato di moto relativo tra emettitore e/o ricevente. L’esempio classico per spiegare l’effetto Doppler è un’ambulanza che passa davanti a un osservatore. Il movimento dell’auto fa sì che le onde sonore davanti all’auto siano compresse e dietro l’auto siano dilatate. L’osservatore (ricevente) percepisce poi questo effetto attraverso la diversa tonalità della sirena: prima che l’ambulanza lo raggiunga, il suono è più alto, non appena l’auto si allontana da lui, il suono è più basso.

A seconda che il emettitore e/o il ricevente si muovano in un mezzo di propagazione- come l’aria – questo cambiamento di frequenza varia. Nella sua lavoro fondamentale “Über das farbige Licht der Doppelsterne und einiger anderen Gestirne des Himmels” pubblicato nel 1842, Doppler ha dato le seguenti formule per calcolare le frequenze percepite dal ricevente.

In queste formule
   è la frequenza percepita dal ricevente
   è la frequenza emessa dall’emettitore
  è la velocità del ricevente rispetto al mezzo di propagazione dell’onda
   è la velocità dell’emettitore rispetto al mezzo di propagazione dell’onda
   è la velocità di propagazione dell’onda nel mezzo (velocità del suono)

Caso 1: ricevente a riposo, emettitore in movimento: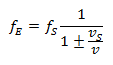

Caso 2: emettitore a riposo, ricevente in movimento: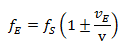

Queste due equazioni descrivono l’effetto Doppler classico. L’effetto del cambiamento di frequenza dipende quindi dalla velocità con cui il emettitore e il ricevente si muovono rispetto al mezzo di propagazione dell’onda. Questa fu una scoperta rivoluzionaria ai tempi di Doppler. Doppler scrisse nella sua opera originale: “Il colore e l’intensità di una sensazione luminosa o l’altezza e la forza di un qualsiasi suono dipendono da queste parametri puramente relativi, non tanto dai valori assoluti.”

 

L’effetto Doppler e la luce

Christian Doppler suppose che questo effetto si applicasse a tutti i tipi di onde. L’ipotesi scientifica dell’epoca era che la luce richiedesse anche un mezzo di propagazione, la cui natura, tuttavia, non era nota e veniva chiamato “etere”. Solo nel 1881 e nel 1887, rispettivamente, i fisici Albert A. Michelson e Edward W. Morley riuscirono a dimostrare sperimentalmente che tale etere non esisteva (esperimento Michelson-Morley). Oggi sappiamo che l’effetto Doppler classico è valido solo per le onde che si propagano in un mezzo di propagazione, come le onde sonore.

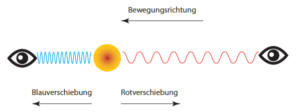
Tuttavia, un effetto Doppler si verifica anche per le onde elettromagnetiche come la luce, che non richiedono un mezzo di propagazione. Questo provoca anche il cambiamento di colore – al blu quando il emettitore si avvicina al ricevente e le onde sono “compresse”, e nel caso opposto al rosso perché le onde sono “dilatate” (vedi illustrazione).

Nel caso delle onde elettromagnetiche, tuttavia, questo effetto non dipende dal movimento relativo tra il mezzo di propagazione e il ricevente o il emettitore, ma solo dal movimento relativo tra il ricevente e il emettitore. Per questo motivo, l’effetto Doppler per le onde luminose è chiamato effetto Doppler relativistico. Per le onde elettromagnetiche, la frequenza ricevuta è legata alla frequenza emessa nel modo seguente:

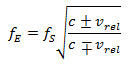
In questa formula per l’effetto Doppler relativistico, c denota la velocità della luce di 299 792 km/s e  la velocità relativa tra il emettitore e il ricevente.

Applicazione pratica della formula Doppler

Negli esempi seguenti, si considerano due casi speciali per la propagazione di un’onda sonora in aria, dove le variabili spiegate sopra sono usate per le frequenze e velocità corrispondenti

Primo caso: Il ricevente sta fermo rispetto all’aria. L’emettitore l’onda sonora si muove con velocità vs in direzione (-) del ricevente o si allontana da esso (+)

In questo caso, la formula di Doppler è:

Un esempio: Un automobilista (emettitore di onde sonore) viaggia a 130 km/h (~36 m/s). Sul bordo della strada sta fermo un pedone (ricevente). Dal momento che i due si conoscono bene, l’automobilista saluta il pedone con un lungo colpo di clacson. La frequenza del sono emesso dall’auto è 1000 Hertz. Quale frequenza viene udita dal pedone?

Durante l’avvicinarsi dell’auto, il pedone sente una frequenza di:

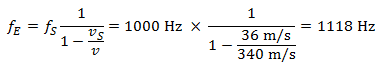
Quando l’auto si allontana, invece, di:

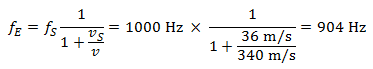
In questo modo quando l’auto si avvicina al pedone la frequenza percepita aumenta di 118 Hertz mentre decresce di 96 Hertz quando l’auto si allontana dal pedone. La frequenza di 1000 Hertz corrisponde circa al Do acuto sopra il rigo (con due tagli addizionali).

Il cambiamento nella frequenza del suono dell’auto è in questo caso abbastanza ridotto ed equivale circa a mezzo tono.

Secondo caso:

L’emettitore dell’onda sonora sta fermo rispetto al mezzo di propagazione (aria). Il ricevente si muove con velocità verso (+) l’emettitore o si allontana (-) da esso.

In questo caso, la formula di Doppler è:

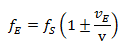
Un esempio: L’automobilista è ora il ricevente e viaggia a 130 km/h (~36 m/s). Sul ciglio della strada sta un pedone fermo con un clacson e saluta il passaggio del suo amico automobilista con un lungo colpo di clacson della frequenza di 1000 Hertz.

Durante l’avvicinamento al pedone l’automobilista sente un suono della frequenza di:

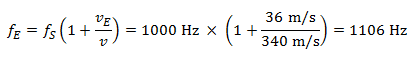
Durante l’allontanamento dal pedone, invece, di

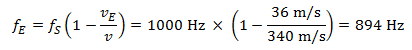
In questo esempio, il cambiamento della frequenza del suono percepito dall’automobilista è in entrambi i casi, di 106 Hertz.

L’origine della differenza nei cambiamenti delle frequenze sonore percepite nei due esempi deriva dal fatto che le onde sonore hanno bisogno di un mezzo di propagazione. Nei due esempi proposti il mezzo è l’aria. Nel primo caso l’emettitore si muove relativamente al mezzo di propagazione, nel secondo caso il ricevente.

Tratto dal libro:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Verlag Anton Pustet 2017

Un ulteriore sguardo sull’effetto Doppler

Tutti conoscono l’effetto Doppler! Ma è proprio così?

Più di 150 anni prima che Christian Doppler descrivesse e formulasse l’effetto che ha poi preso il suo nome, l’astronomo danese O. Rømer ed i suoi colleghi lo avevano già utilizzato per determinare la velocità della luce.

È generalmente conosciuto che l’effetto Doppler descrive il cambiamento della frequenza di un’onda così come viene misurato nel caso in cui trasmittente e ricevente si trovino in uno stato di moto relativo l’uno rispetto all’altro. Il risultato dell’osservazione è quindi la descrizione di un fenomeno cinematico.

C’è assoluto bisogno di un’onda come mezzo di comunicazione tra trasmittente e ricevente? No: c’è anche un’altra possibilità , e cioè l’effetto “Doppler-Faro”. In un faro una lampada ruota con una velocità angolare costante. Un osservatore stazionario ad una certa distanza rispetto al faro noterà gli impulsi luminosi brevi in una frequenza regolare. Avvicinandosi al faro, l’osservatore misurerà una frequenza degli impulsi luminosi maggiore, mentre allontanandosene, la frequenza misurata diminuirà – esattamente come nel caso dell’effetto Doppler “classico” nel caso della frequenza delle onde. Nella pratica quotidiana l’effetto Doppler-Faro non è però rilevante dal momento che gli osservatori si muovono, di regola, lentamente (ad esempio, navi).

Come già accennato prima, questo effetto “Doppler-Faro” era già stato applicato da tempo nell’astronomia. Il primo, seppur straordinario, esempio: al tempo di Rømer, cioè alla fine del XVII secolo, grazie alle leggi di Keplero sul moto dei pianeti, le velocità di rivoluzione dei pianeti del sistema solare e con esse sia le distanze relative che le velocità dei pianeti erano ben conosciute. Contemporaneamente, Galilei aveva scoperto le quattro lune medicee del pianeta Giove. Inoltre, si era riusciti a misurare il periodo di rivoluzione di Io, la luna più vicina a Giove, osservando il suo periodico scomparire dietro a Giove ed il suo successivo ricomparire alla vista.¹ Dopo alcuni anni di osservazioni accurate ci si rese però conto che questa velocità di rivoluzione variava nel corso dell’anno! Dal momento che la validità della meccanica newtoniana era fuori discussione, bisognava cercare un’altra spiegazione di questo fenomeno.

A questo punto Rømer ebbe la gloriosa idea che la luce, che ci trasmette il segnale della sparizione e successiva ricomparsa di Io, potesse avere una velocità di propagazione finita e che il fenomeno osservato potesse essere spiegato tenendo conto della velocità della terra rispetto a Giove, dal momento che quest’ultima varia durante un anno. La Terra è più vicina al Sole di Giove, per questo motivo la sua velocità angolare attorno al Sole è maggiore di quella di Giove. Per un certo tempo la Terra si avvicina a Giove, poi lo supera, e successivamente se ne allontana. L’osservazione di Io è perciò un caso dell’effetto “Doppler-Faro”. La prima misura della velocità di propagazione della luce non fu molto accurata, però del giusto ordine di grandezza, cosa che meravigliò moltissimo molti fisici del tempo.

Un secondo, più recente, esempio è parimenti molto impressionante. La Pulsar PSR1913+16 effettua 17 rotazioni al secondo attorno a sé stessa ed emette degli impulsi radio in un ben definito angolo solido. Quando questo angolo solido è rivolto verso la terra, i radiotelescopi terrestri ricevono un impulso radio della durata di qualche millisecondo. Se la Pulsar, che dista dalla Terra circa 22000 anni-luce, fosse ferma rispetto al Sole, allora la frequenza di ricezione degli impulsi radio sulla Terra dovrebbe variare in maniera sincrona con la rivoluzione della Terra attorno al Sole. Le variazioni osservate dei tempi di ricezione degli impulsi e delle loro frequenze sono, viceversa, sensibilmente più rapide, maggiori e più frequenti.

R. Hulse e J. Taylor rifecero nella seconda metà del XX secolo quello che i fisici avevano già fatto alla fine del XVII secolo. Essi riuscirono a spiegare i tempi di ricezione dei impulsi radio e le loro variazioni col fatto che PSR1913+16 costituisce, assieme ad una stella di neutroni, un sistema binario: questi due oggetti percorrono traiettorie ellittiche attorno al centro di gravità comune del sistema con un periodo di rivoluzione pari a 7.75 ore.² La velocità orbitale delle due stelle è nel punto in cui le stelle sono più vicine quattro volte maggiore di quella posseduta dalle stelle nel punto di massima distanza relativa– fatto ideale per l’osservazione delle variazioni degli intervalli di tempo tra gli impulsi radio che rappresentano il “faro” per questo effetto Doppler. Nel frattempo, le misure sono diventate così precise che questo sistema binario viene usato per effettuare dei test sulla teoria generale della relatività, tra i quali la rapida precessione delle orbite e la diminuzione dei parametri orbitali della Pulsar causata dall’emissione di onde gravitazionali. Le misure di Hulse e Taylor assieme alla loro interpretazione furono giustamente premiate nel 1993 col premio Nobel per la fisica. Nel frattempo, questo orologio a radio impulsi super preciso e’ stato strumentale per determinare più precisamente la velocità del movimento del Sole attorno al centro della nostra Via Lattea.

Forse, a prima vista, la differenza tra un effetto Doppler “classico” ed un effetto “Doppler-Faro” non risulti evidente. Il fatto che anche nell’effetto “Doppler-Faro” il segnale misurato consiste, nella maggioranza dei casi, da onde elettromagnetiche (la luce visibile di Io ed un segnale radio ad ampia banda nel caso di PSR1913+16) potrebbe causare confusione. Quello che viene misurato nell’effetto “Doppler-Faro” non è il cambiamento della frequenza dell’onda elettromagnetica (che non sarebbe praticamente misurabile a causa della ampiezza dello spettro della luce visibile o delle onde radio), ma il tempo di arrivo dei segnali elettromagnetici (impulsi). Per poter effettuare una misura significativa, la durata temporale dell’impulso deve essere molto minore dell’intervallo di tempo di ricezione dei segnali successivi. (Questo accade in entrambi i casi descritti). Quando il ricevente si avvicina a velocità costante ad un faro (oppure il faro al ricevente), allora gli intervalli tra due segnali consecutivi si accorciano rispetto al caso stazionario, dal momento che lo spazio che la luce deve percorrere tra due segnali successivi diminuisce.

Già da tempo gli astronomi chiamano in maniera disinvolta “Effetto Doppler” queste variazioni degli intervalli tra segnali successivi che dipendono dalla velocità relativa tra trasmittente e ricevente. Alcuni fisici esitano a farlo perché ritengono che solamente le variazioni delle frequenze delle onde possano essere chiamate “Effetto Doppler”. Ma una disputa sulle definizioni sembra inutile. Visto che il risultato finale è la misura della velocità relativa tra trasmittente e ricevente, è irrilevante se per ottenere questo risultato si misura la variazione di frequenza di un’onda (effetto Doppler “classico”) oppure degli intervalli del tempo di ricezione fra segnali periodici successivi (effetto Doppler “Faro”). La denominazione “Effetto-Doppler” è appropriata in entrambi i casi, anche se lo stesso Doppler non aveva pensato a questa generalizzazione. Nella sua pubblicazione originale del 1842, Doppler parlava di “impatti d’onda” e derivò dalla variazione del numero di impatti per unita’ temporale tra trasmittente e ricevente le formule dell’effetto Doppler. Queste formule sono valide per qualunque sorgente di “impatti d’onda”, quindi anche per i “segnali-Faro”.

Further information on the Doppler effect | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
²  https://de.wikipedia.org/wiki/PSR_J1915%2B1606