Efeito Doppler

A física do Efeito Doppler

O efeito Doppler descreve a alteração da frequência de uma onda, dependendo do estado de movimento da sua fonte e/ou receptor. O exemplo clássico para explicar o efeito Doppler é o de uma ambulância que passa por um observador. Devido ao movimento do veículo, as ondas sonoras são comprimidas à frente do carro e alongadas atrás dele. O observador percebe esse efeito pela variação na frequência do som da sirene: antes de a ambulância chegar até ele, o som é mais agudo, e à medida que o veículo se afasta, o som se torna mais grave.

Dependendo se o emissor e/ou o receptor se movem num meio — como, por exemplo, o ar — essa alteração na frequência tem diferentes magnitudes. Na sua obra fundamental de 1842, intitulada “Sobre a luz colorida das estrelas duplas e de alguns outros astros do céu”, Doppler apresentou as seguintes fórmulas para o cálculo das frequências percebidas pelo receptor.

Nessas fórmulas:

   representa a frequência percebida pelo receptor,
   representa a frequência emitida pelo emissor,
   representa a velocidade do receptor em relação ao meio,
   representa a velocidade do emissor em relação ao meio, e
   representa a velocidade de propagação da onda no meio (velocidade do som).

Caso 1: Receptor está em repouso, emissor move-se: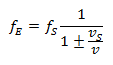

Caso 2: Emissor está em repouso, receptor move-se: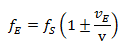

Essas duas equações descrevem o efeito Doppler clássico. Assim, a magnitude da mudança de frequência depende da velocidade com que o emissor e o receptor se movem em relação ao meio de propagação da onda. Essa foi uma descoberta revolucionária na época de Doppler. Em sua obra original, Doppler escreveu: “A cor e a intensidade de uma sensação luminosa ou a frequência e intensidade de qualquer som dependem dessas determinações puramente subjetivas, e não da sua situação objetiva.”

O efeito Doppler e a luz

Christian Doppler presumiu que esse efeito seria aplicável a qualquer tipo de onda. Na época, a ciência acreditava que a luz também necessitava de um meio de propagação, cuja natureza, no entanto, não era conhecida e era denominada “éter”. Somente em 1881 e, posteriormente, em 1887, os físicos Albert A. Michelson e Edward W. Morley conseguiram demonstrar experimentalmente que tal éter como meio de propagação da luz não existia (experiência de Michelson-Morley). Hoje, sabe-se que o efeito Doppler clássico é válido apenas para ondas que se propagam num meio.

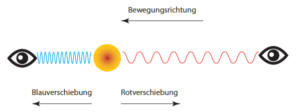
O efeito Doppler ocorre também para ondas eletromagnéticas, como a luz, que não necessitam de um meio de propagação. Isso resulta no fenómeno conhecido como desvio para o azul, quando o emissor se aproxima do receptor e as ondas são ‘comprimidas’, e no desvio para o vermelho, quando as ondas são ‘esticadas’ no caso oposto. (ver figura).

No caso das ondas eletromagnéticas, esse efeito não depende da movimentação relativa entre o meio de propagação e o receptor ou o emissor, mas apenas da movimentação relativa entre o receptor e o emissor. Por essa razão, o efeito Doppler para ondas luminosas é denominado efeito Doppler relativístico. Para ondas eletromagnéticas, a frequência recebida está relacionada à frequência emitida da seguinte forma:

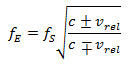
Nessa fórmula para o efeito Doppler relativístico, c representa a velocidade da luz, que é 299.792 km/s, e a velocidade relativa entre o emissor e o receptor.

Aplicação prática da fórmula de Doppler

Nos exemplos a seguir, dois casos especiais de propagação de uma onda sonora no ar são considerados, em que as variáveis explicadas acima para as respectivas frequências e velocidades são aplicadas à fórmula de Doppler

Caso 1: O receptor está em repouso em relação ao ar, e o emissor (fonte sonora) move-se com a velocidade  em direção ao receptor (-) ou afastando-se dele (+).

A fórmula de Doppler neste caso é:

Exemplo: Um motorista (emissor da onda sonora) passa a 130 km/h (~36 m/s) por um pedestre parado na calçada (receptor das ondas sonoras). Como o motorista e o pedestre se conhecem bem, o motorista cumprimenta o pedestre com uma longa buzina. A frequência da buzina é de 1.000 hertz. Qual é a frequência percebida pelo pedestre?

O pedestre ouve uma frequência mais alta durante a aproximação do carro:

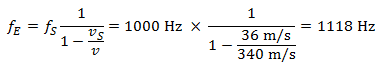
Quando o carro se afasta do receptor, a frequência do som cai:

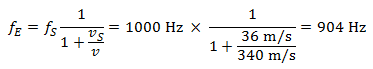
Assim, ao se aproximar do pedestre, a frequência aumenta em 118 hertz e, ao se afastar, cai em 96 hertz. A frequência de 1.000 hertz corresponde aproximadamente ao ‘dó alto’, que está duas linhas acima no sistema de cinco linhas da pauta musical. As variações de frequência ao se aproximar e ao se afastar do pedestre são ligeiramente diferentes e equivalem, neste caso, a cerca de meio tom.

Caso 2: O emissor (fonte sonora) está em repouso em relação ao ar, e o receptor move-se com a velocidade em direção ao emissor (+) ou afastando-se dele (-).

A fórmula de Doppler neste caso é:

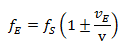
Exemplo: O motorista agora é o receptor e passa a 130 km/h (~36 m/s) pelo conhecido parado na calçada (emissor), que por acaso tem uma buzina e o cumprimenta com um longo som de buzina de 1.000 hertz.

O motorista ouve, ao se aproximar, um som com uma frequência de:

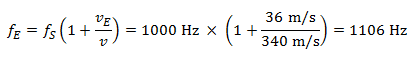
Ao se afastar do pedestre, ele ouve um som com uma frequência de:

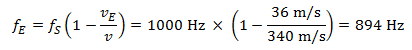
Neste caso, a variação de frequência percebida pelo receptor (motorista) ao se aproximar e se afastar do conhecido é a mesma, sendo de 106 hertz em cada caso.

A razão para a diferença nas variações de frequência nos dois casos é que o som precisa de um meio de propagação. Neste exemplo, esse meio é o ar. No caso 1, o emissor (a fonte sonora) move-se em relação ao ar; no caso 2, é o receptor que se move.

Baseado no livro:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Verlag Anton Pustet 2017.

 

Um olhar mais aprofundado sobre o efeito Doppler

Todo mundo conhece o efeito Doppler! Será mesmo?

Mais de 150 anos antes de Christian Doppler descrever o efeito que leva seu nome e formular suas equações, O. Rømer e seus colegas já o utilizavam para determinar a velocidade da luz.

É de conhecimento geral na física que o efeito Doppler descreve a variação da frequência das ondas quando o emissor e o receptor se movem um em relação ao outro. O que se observa é, portanto, a descrição de um fenómeno dinâmico. Mas será que é sempre necessário haver uma onda como meio de comunicação entre o emissor e o receptor? Não; há outra maneira, exemplificada pelo efeito Doppler do farol.
Num farol, um feixe de luz gira com uma velocidade angular constante. Um observador estacionário a uma certa distância vê, com frequência regular, um breve pulso de luz. Se o observador se aproximar ou se afastar do farol, a frequência com que ele recebe os pulsos de luz aumenta ou diminui, exatamente como acontece no efeito Doppler “clássico”, em que a frequência de uma onda se altera. Na prática, isso é difícil de perceber, pois os observadores (como navios) se movem apenas lentamente.

Como já mencionado acima, esse efeito Doppler do farol é utilizado na astronomia há muito tempo. Um exemplo interessante, embora incomum, vem da época de Rømer. No final do século XVII, as velocidades orbitais dos planetas ao redor do Sol já eram bem conhecidas graças às leis de Kepler, assim como as suas distâncias relativas e as velocidades em relação uns aos outros. Galileu havia descoberto os quatro maiores satélites de Júpiter. Em particular, o período orbital de Io, a lua mais interna, podia ser medido observando o seu desaparecimento e reaparecimento regular por trás de Júpiter.

Após alguns anos de observação cuidadosa, no entanto, descobriu-se que essa velocidade orbital variava ao longo de um ano! Como as leis de Newton eram incontestáveis, era necessária outra explicação para esse fenômeno. Rømer teve então a brilhante ideia de que a luz, que transmite o “sinal” do desaparecimento ou reaparecimento de Io, poderia ter uma velocidade finita, e o fenômeno poderia ser explicado pela conhecida velocidade da Terra em relação a Júpiter, que varia ao longo do ano. A Terra, estando mais próxima do Sol, move-se mais rapidamente do que Júpiter, aproximando-se de Júpiter em certos momentos e afastando-se em outros. As observações de Io estão, portanto, sujeitas ao efeito Doppler do farol!

A primeira determinação da velocidade da luz não foi muito precisa, mas estava na ordem de grandeza correta, o que surpreendeu muitos físicos da época.

Um segundo exemplo mais recente é igualmente impressionante. O pulsar PSR1913+16 gira 17 vezes por segundo e emite pulsos de rádio num cone bem definido. Quando esse cone cruza a Terra, os nossos radiotelescópios detectam um pulso de rádio com duração de poucos milissegundos. Se o pulsar (localizado a cerca de 22.000 anos-luz) estivesse estacionário, a frequência dos pulsos variaria apenas no ritmo da órbita da Terra ao redor do Sol. No entanto, as variações nos tempos de chegada dos pulsos e nas suas frequências são muito mais rápidas e frequentes.

O que os físicos do final do século XVII fizeram, R. Hulse e J. Taylor repetiram na segunda metade do século XX. Eles puderam explicar as variações nas chegadas dos pulsos de rádio observando que PSR1913+16 forma um sistema binário com outra estrela de nêutrons, e que ambas orbitam com grande velocidade ao redor de um centro de massa comum, com um período orbital de apenas 7,75 horas. A velocidade orbital é quatro vezes maior no ponto de maior aproximação entre as estrelas do que no ponto de maior afastamento — ideal para observar a mudança dos intervalos entre os pulsos de rádio, que funcionam como um “farol” para esse efeito Doppler.

As medições são tão precisas que esse sistema binário se tornou um objeto de teste para os efeitos da Teoria da Relatividade Geral, incluindo a rápida precessão das órbitas e a diminuição dos parâmetros orbitais do pulsar devido à emissão de ondas gravitacionais. Hulse e Taylor receberam o Prêmio Nobel de Física em 1993 pelas suas medições e interpretações. Desde então, esse relógio superpreciso dos pulsos de rádio ajudou a medir com maior precisão a velocidade de movimento do Sol em torno do centro da nossa galáxia, a Via Láctea.

À primeira vista, a diferença entre um efeito Doppler “clássico” e um “efeito Doppler do farol” pode não ser óbvia. O facto de que, em muitos casos, o sinal também é transmitido por uma onda eletromagnética (como a luz visível de Io ou os sinais de rádio de PSR1913+16) pode causar confusão. No entanto, o que é medido no efeito Doppler do farol não é a mudança de frequência da radiação (que é praticamente impossível de medir devido ao espectro amplo das ondas de luz ou rádio), mas sim o tempo exato de chegada dos sinais (pulsos). Para ser significativo, a duração do pulso deve ser muito mais curta do que o intervalo de tempo entre sinais consecutivos. (Isso é o caso nos dois exemplos descritos acima.)

Se um observador se aproxima de um farol a uma velocidade constante (ou se a fonte de sinais se aproxima do observador), os intervalos entre os sinais consecutivos serão mais curtos do que se estivesse em repouso, pois a luz percorre uma distância menor entre os sinais.

Os astrônomos há muito tempo chamam essas variações dos intervalos entre sinais consecutivos, em função das velocidades relativas entre o emissor e o receptor, de efeito Doppler. Alguns físicos hesitam em usar esse termo, pois acreditam que apenas mudanças na frequência das ondas deveriam ser chamadas de “efeito Doppler”. Contudo, discutir definições é fútil. Como o objetivo final é medir as velocidades relativas entre emissor e receptor, não importa se isso é feito medindo a mudança na frequência de uma onda (efeito Doppler “clássico”) ou medindo os intervalos de tempo entre os pulsos de sinais sucessivos (efeito “farol”). O termo efeito Doppler é adequado para ambos, embora Doppler não tivesse em mente essa generalização em sua época. Em sua publicação original de 1842, Doppler falou de “batidas de ondas” e derivou suas fórmulas a partir da diferença no número de batidas por unidade de tempo entre o emissor e o receptor. Suas fórmulas, portanto, se aplicam a qualquer fonte de “batidas”, incluindo os sinais de um “farol”.

Informações adicionais sobre o efeito Doppler | hyperphysics.phy-astr.gsu.edu

¹ J.M. Shea, Am.J.Phys, 7/66, 1998, p. 569
² https://de.wikipedia.org/wiki/PSR_J1915%2B1606